题目内容
19. 如图,正方形OABC在平面直角坐标系中,点A的坐标为(2,0),将正方形OABC绕点O顺时针旋转45°,得到正方形OA′B′C′,则点C′的坐标为( )
如图,正方形OABC在平面直角坐标系中,点A的坐标为(2,0),将正方形OABC绕点O顺时针旋转45°,得到正方形OA′B′C′,则点C′的坐标为( )| A. | ($\sqrt{2}$,$\sqrt{2}$) | B. | (-$\sqrt{2}$,$\sqrt{2}$) | C. | ($\sqrt{2}$,$-\sqrt{2}$) | D. | (2$\sqrt{2}$,2$\sqrt{2}$) |
分析 先根据点A的坐标求出正方形的边长,再根据旋转可得点C′在第一象限的平分线上,然后求解即可.
解答 解:∵点A的坐标为(2,0),
∴正方形OABC的边长为2,
∵正方形OABC绕点O顺时针旋转45°,得到正方形OA′B′C′,
∴点C′在第一象限的平分线上,
∴点C′的横坐标为2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$,
纵坐标为为2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$,
∴点C′的坐标为($\sqrt{2}$,$\sqrt{2}$).
故选A.
点评 本题考查了坐标与图形变化-旋转,正方形的性质,熟记性质并判断出点C′的位置是解题的关键.

练习册系列答案
相关题目
12.如图所示,在平面直角坐标系中A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,把△AP1B绕点B顺时针旋转180°,得到△BP2C;把△BP2C绕点C顺时针旋转180°,得到△CP3D.依此类推,则旋转第2015次后,得到的等腰直角三角形的直角顶点P2016的坐标为( )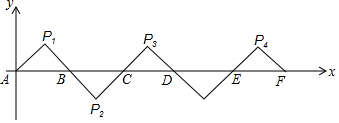

| A. | (4033,-1) | B. | (4031,-1) | C. | (4033,1) | D. | (4031,1) |
12.在△ABC中,∠A+∠B=90°,则△ABC是( )
| A. | 锐角三角形 | B. | 钝角三角形 | ||
| C. | 直角三角形 | D. | 钝角三角形或直角三角形 |
7.我们在学习有理数乘法运算时研究了下面的问题.规定:水位上升为正,水位下降为负;几天后为正,几天前为负,若水位每天下降4cm,今天的水位记为0cm,那么3天前的水位用算式表示正确的是( )
| A. | (+4)×(+3) | B. | (-4)×(-3) | C. | (+4)×(-3) | D. | (-4)×(+3) |
14. 如图,直线a∥b,直线l与a,b分别相交于A,B两点,AC⊥AB交b于点C,∠1=40°,则∠2的度数是( )
如图,直线a∥b,直线l与a,b分别相交于A,B两点,AC⊥AB交b于点C,∠1=40°,则∠2的度数是( )
 如图,直线a∥b,直线l与a,b分别相交于A,B两点,AC⊥AB交b于点C,∠1=40°,则∠2的度数是( )
如图,直线a∥b,直线l与a,b分别相交于A,B两点,AC⊥AB交b于点C,∠1=40°,则∠2的度数是( )| A. | 40° | B. | 45° | C. | 50° | D. | 60° |
4. 如图,在正方形ABCD中,O为对角线交点,将扇形AOD绕点O顺时针旋转一定角度得到扇形EOF,则在旋转过程中图中阴影部分的面积( )
如图,在正方形ABCD中,O为对角线交点,将扇形AOD绕点O顺时针旋转一定角度得到扇形EOF,则在旋转过程中图中阴影部分的面积( )
 如图,在正方形ABCD中,O为对角线交点,将扇形AOD绕点O顺时针旋转一定角度得到扇形EOF,则在旋转过程中图中阴影部分的面积( )
如图,在正方形ABCD中,O为对角线交点,将扇形AOD绕点O顺时针旋转一定角度得到扇形EOF,则在旋转过程中图中阴影部分的面积( )| A. | 不变 | B. | 由大变小 | ||
| C. | 由小变大 | D. | 先由小变大,后由大变小 |
 写出数轴上点A、点B、点C所表示的分数:$\frac{1}{4}$,1$\frac{3}{4}$,2$\frac{5}{8}$.
写出数轴上点A、点B、点C所表示的分数:$\frac{1}{4}$,1$\frac{3}{4}$,2$\frac{5}{8}$. 如图,在平行四边形ABCD中,∠A的平分线交BC于点F,若AB=10 cm,AD=16 cm,则FC=6cm.
如图,在平行四边形ABCD中,∠A的平分线交BC于点F,若AB=10 cm,AD=16 cm,则FC=6cm.