题目内容
18.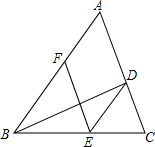 如图,BD是△ABC的角平分线,点E,F分别在边BC,AB上,且DE∥AB,BE=AF.
如图,BD是△ABC的角平分线,点E,F分别在边BC,AB上,且DE∥AB,BE=AF.(1)求证:EF∥AC;
(2)若∠ABC=56°,∠ADB=120°,求∠AFE的度数.
分析 (1)利用等角对等边证明BE=DE,然后证得DE=AF且DE∥AF,据此即可证得四边形AFED是平行四边形,再根据平行四边形的定义证得EF∥AC;
(2)求得∠ADE的度数,然后根据平行四边形的对角相等即可求解.
解答 解:(1)∵DE∥AB,
∴∠ABD=∠BDE,
又∵BD是△ABC的平分线,即∠ABD=∠DBC,
∴∠BDE=∠DBE,
∴BE=DE,
又∵BE=AF,
∴DE=AF,
又∵DE∥AF,
∴四边形AFED是平行四边形,
∴EF∥AC;
(2)∵∠BDE=∠ABD=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×56°=28°,
又∵∠ADB=120°,
∴∠ADE=120°+28°=148°,
∵四边形AFED是平行四边形,
∴∠AFE=∠ADE=148°.
点评 本题考查了平行四边形的判定与性质,证明DE=AF是解题的关键.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
8.在△ABC中,AB=AC,∠BAC=50°,则∠C的度数为( )
| A. | 75° | B. | 65° | C. | 55° | D. | 50° |
 如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论:
如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论: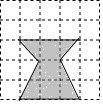 如图,方格图中小正方形的边长为1.将方格图中阴影部分图形剪下来,再把剪下的阴影部分重新剪拼成一个正方形(不重叠无缝隙),那么所拼成的这个正方形的边长为$\sqrt{6}$.
如图,方格图中小正方形的边长为1.将方格图中阴影部分图形剪下来,再把剪下的阴影部分重新剪拼成一个正方形(不重叠无缝隙),那么所拼成的这个正方形的边长为$\sqrt{6}$.