题目内容
15.解方程:|2-x|-|x+2|=4.分析 分别讨论①x≤-2,②-2<x≤2,③x>2,根据x的范围去掉绝对值,解出x,综合三种情况可得出x的最终范围.
解答 解:当x≤-2时,原式即2-x+x+2=4,则对于任何数都是方程的解;
当-2<x≤2时,原式即2-x-(x+2)=4,即2-x-x-2=4,解得x=-2(舍去);
当x>2时,原式即x-2-(x+2)=4,不成立.
总之,x≤-2的任意数都是方程的解.
点评 本题考查了含绝对值符号的一元一次方程,分类讨论是解题关键,意最后的解可以联合起来,难度很大.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
3.如果一元一次方程3x-b=0的根x=2,那么一次函数y=3x-b的图象一定过点( )
| A. | (0,2) | B. | (2,0) | C. | (-2,0) | D. | (0,-2) |
4.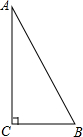 如图,Rt△ABC,∠C=90°,AB=13,BC=5,则cosB的值为( )
如图,Rt△ABC,∠C=90°,AB=13,BC=5,则cosB的值为( )
 如图,Rt△ABC,∠C=90°,AB=13,BC=5,则cosB的值为( )
如图,Rt△ABC,∠C=90°,AB=13,BC=5,则cosB的值为( )| A. | $\frac{5}{13}$ | B. | $\frac{12}{13}$ | C. | $\frac{5}{12}$ | D. | $\frac{13}{3}$ |
5.资料显示2013年上半年台州市全年财政总收入为242亿元,将242亿元保留2个有效数字可表示为( )
| A. | 240000000000元 | B. | 2.42×108元 | C. | 2.4×109元 | D. | 2.4×1010元 |
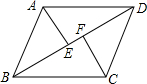 如图,在?ABCD中,E、F是对角线BD上的两点,且BE=DF,连接AE、CF,问:AE与CF相等吗?并说明理由.
如图,在?ABCD中,E、F是对角线BD上的两点,且BE=DF,连接AE、CF,问:AE与CF相等吗?并说明理由.