题目内容
2．
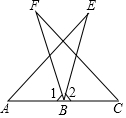如图，已知AB=CB，BE=BF，点A，B，C在同一条直线上，∠1=∠2．（1）证明：△ABE≌△CBF；
（2）若∠FBE=40°，∠C=45°，求∠E的度数．
分析 （1）根据SAS即可证明；
（2）在△ABE中，求出∠A，∠ABE即可解决问题；
解答 （1）证明：∵∠1=∠2，
∴∠ABE=∠CBF，
在△ABE和△CBF中，
$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠CBF}\\{BE=BF}\end{array}\right.$，
∴△ABE≌△CBF．
（2）解：∵∠1=∠2，∠FBE=40°，
∴∠1=∠2=70°，
∵△ABE≌△CBF，
∴∠A=∠C=45°，
∵∠ABE=∠1+∠FBE=110°，
∴∠E=180°-∠A-∠ABE=25°．
点评 本题考查全等三角形的判定和性质，三角形的内角和定理等知识，解题的关键是灵活运用所学知识解决问题，属于中考常见题．
练习册系列答案
阅读快车系列答案
相关题目
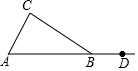如图，在△ABC中，AB=BC，点D在AB的延长线上．
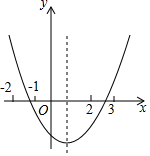如图，图中二次函数解析式为y=ax2+bx+c（a≠0）则下列命题中正确的有①③④（填序号）
