题目内容
在一个多边形中，小于120°的内角不能多于 个．
考点：多边形内角与外角
专题：
分析：先由多边形的每个内角小于120°求出每一个外角大于60°，再根据多边形的外角和为360°，可知边数≤360°÷60°．
解答：解：∵多边形的内角小于120°，
∴外角大于60°，
∴这个多边形小于120°的内角的个数≤360°÷60°=6．
故答案为：6．
∴外角大于60°，
∴这个多边形小于120°的内角的个数≤360°÷60°=6．
故答案为：6．
点评：本题主要考查了多边形的内角与外角的关系及多边形的外角和定理，求出每一个外角的度数范围是关键．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
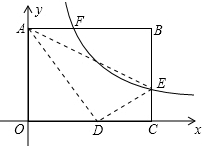矩形OABC在平面直角坐标系中如图，已知AB=10，BC=8，EB是C上一点，将△ABE沿AE折叠，点B刚好与OC边上点D重合，过点E的反比例函数y=| k |
| x |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
如果a＞b＞0，c＞d＞0，则一定有（ ）
| A、ab-cd＞0 |
| B、bc-ad＞0 |
| C、cd-ab＞0 |
| D、ac-bd＞0 |
已知线段AB，求作线段OC，使OC=AB．
如图，在△ABC中，AD是BC边上的中线，sinB=
如图，点O是△ABC内任意一点，连接AO、BO、CO，点E、F、D分别是BO、CO、AO的中点，求证：△EDF∽△BAC．