题目内容
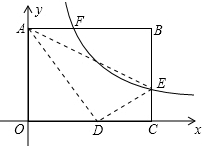 矩形OABC在平面直角坐标系中如图,已知AB=10,BC=8,EB是C上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=
矩形OABC在平面直角坐标系中如图,已知AB=10,BC=8,EB是C上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=| k |
| x |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
考点:反比例函数综合题
专题:
分析:首先根据折叠的性质得到BE=DE,AB=AD,∠ABE=∠ADE=90°,然后利用勾股定理求得OD的长,从而得到DC=OC-OD=10-6=4,设点E的坐标为(10,
),则可以表示EC=
,BE=ED=8-
,然后在Rt△ECD中,利用勾股定理42+(
)2=(8-
)2,解得k值后即可求得反比例函数的解析式,代入y=8后求得x的值即可求得AF.
| k |
| 10 |
| k |
| 10 |
| k |
| 10 |
| k |
| 10 |
| k |
| 10 |
解答:解:∵将△ABE沿AE折叠,点B刚好与OC边上点D重合,
∴BE=DE,AB=AD,∠ABE=∠ADE=90°,
∵AB=10,BC=8,
∴AO=BC=8,AD=AB=10,
∴由勾股定理得:OD=
=
=6,
∴DC=OC-OD=10-6=4,
设点E的坐标为(10,
),
∴EC=
,BE=ED=8-
,
在Rt△ECD中,
DC2+EC2=DE2,
即:42+(
)2=(8-
)2,
解得:k=30,
∴反比例函数的解析式是y=
,
令y=8,
解得:x=
,
∴AF=
,
故选B.
∴BE=DE,AB=AD,∠ABE=∠ADE=90°,
∵AB=10,BC=8,
∴AO=BC=8,AD=AB=10,
∴由勾股定理得:OD=
| AD2-AO2 |
| 102-82 |
∴DC=OC-OD=10-6=4,
设点E的坐标为(10,
| k |
| 10 |
∴EC=
| k |
| 10 |
| k |
| 10 |
在Rt△ECD中,
DC2+EC2=DE2,
即:42+(
| k |
| 10 |
| k |
| 10 |
解得:k=30,
∴反比例函数的解析式是y=
| 30 |
| x |
令y=8,
解得:x=
| 15 |
| 4 |
∴AF=
| 15 |
| 4 |
故选B.
点评:本题考查了反比例函数的综合知识,还涉及到了折叠问题、勾股定理等知识,综合性强,难度中等偏上.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
下列各组数中,互为相反数的是( )
| A、+(-3)和-(-3) |
| B、-(-3)和﹢3 |
| C、-1 和-12 |
| D、-|-2|和-2 |
 已知,如图,点D为△ABC的边AB的中点,点E为AC上一点,AE=2CE,BE和CD相交于点O.求证:OE=
已知,如图,点D为△ABC的边AB的中点,点E为AC上一点,AE=2CE,BE和CD相交于点O.求证:OE=