题目内容
14.在直角△ABC中∠ACB=90°,∠A=30°,AB=4,点D、E分别在AB、AC边上,将∠A沿DE折叠,使点A落在三角形内部(不含边界)的点P处,连接PB、PC.设P到直线DE的距离d.若△PBC是直角三角形,则d的取值范围是$\frac{\sqrt{13}-2}{2}$$≤d<\sqrt{3}$.分析 以BC为直径作⊙O,由直径所对的圆周角是90°可知三角形△PBC是直角三角形,在直角△ABC中∠ACB=90°,∠A=30°,AB=4,可知BC=2,AC=2$\sqrt{3}$,由翻折的性质可知:d=PF=$\frac{1}{2}AP$,当点P在AO于圆的交点处时,d有最小值,当点P与点C重合时,d有最大值,从而可求得d的取值范围.
解答 解:以BC为直径作⊙O.
∵BC为⊙O的直径,
∴∠BPC=90°,
∵∠ACB=90°,∠A=30°,AB=4,
∴BC=2.
在Rt△ABC中,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$.
由翻折的性质可知:PA⊥DE,PF=AF.
∴d=PF=$\frac{1}{2}AP$.
如图1所示: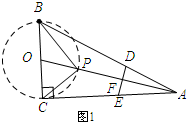
OA=$\sqrt{O{C}^{2}+A{C}^{2}}$=$\sqrt{{1}^{2}+(2\sqrt{3})^{2}}$=$\sqrt{13}$,
∴PA=AO-OP=$\sqrt{13}$-2.
∴d=$\frac{1}{2}AP=\frac{\sqrt{13}-2}{2}$.
如图2所示: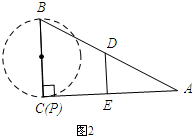
当点P与点C重合时,PA=AC=2$\sqrt{3}$,
∴d=$\frac{1}{2}AP$=$\frac{1}{2}×2\sqrt{3}$=$\sqrt{3}$.
∵点P不在边界上,故d<$\sqrt{3}$.
∴d的取值范围是$\frac{\sqrt{13}-2}{2}$$≤d<\sqrt{3}$.
故答案为:$\frac{\sqrt{13}-2}{2}$$≤d<\sqrt{3}$.
点评 本题主要考查的是翻折的性质、勾股定理、含30°直角三角形的性质,根据题意作出圆O是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,ABCDE是正五边形,AP,AQ和AR是由A向CD,CB和DE的延长线上所引的垂线,设O是正五边形的中心,若OP=1,则AO+AQ+AR等于( )
如图,ABCDE是正五边形,AP,AQ和AR是由A向CD,CB和DE的延长线上所引的垂线,设O是正五边形的中心,若OP=1,则AO+AQ+AR等于( )| A. | 3 | B. | 1+$\sqrt{5}$ | C. | 4 | D. | 2+$\sqrt{5}$ | ||||
| E. | 5 |
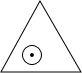 如图,一个半径为1的圆形纸片在边长为a(a≥2$\sqrt{3}$)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )
如图,一个半径为1的圆形纸片在边长为a(a≥2$\sqrt{3}$)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )| A. | $\frac{π}{3}$ | B. | $\frac{3\sqrt{3}-π}{3}$ | C. | 3$\sqrt{3}$-π | D. | 不能求出具体值 |
| A. | (x-2)2=-3 | B. | (x-2)2=3 | C. | (x+2)2=-3 | D. | (x+2)2=3 |
 在直角梯形ABCD中,AD∥BC,∠ADC=90°,AB=5,AD=8,CD=3,线段AD上有一动点E,过点E作EF⊥AB,垂足为点F.
在直角梯形ABCD中,AD∥BC,∠ADC=90°,AB=5,AD=8,CD=3,线段AD上有一动点E,过点E作EF⊥AB,垂足为点F. 如图,D为△ABC内的一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若CF=6,BF=9,AG=8,则△ADC的面积为24.
如图,D为△ABC内的一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若CF=6,BF=9,AG=8,则△ADC的面积为24.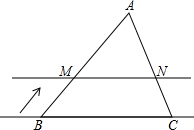 如图,在△ABC中,AB=7,AC=$\sqrt{17}$,BC=8,线段BC所在直线以每秒2个单位的速度沿BA方向运动,并始终保持与原位置平行.该直线与AB、AC分别交于点M、N,记x秒时,并设△AMN中MN边上的高为y.试写出y关于x的函数关系式y=-2x+$\sqrt{13}$,自变量x的取值范围是0<x<$\sqrt{13}$.
如图,在△ABC中,AB=7,AC=$\sqrt{17}$,BC=8,线段BC所在直线以每秒2个单位的速度沿BA方向运动,并始终保持与原位置平行.该直线与AB、AC分别交于点M、N,记x秒时,并设△AMN中MN边上的高为y.试写出y关于x的函数关系式y=-2x+$\sqrt{13}$,自变量x的取值范围是0<x<$\sqrt{13}$.