题目内容
3．
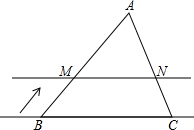如图，在△ABC中，AB=7，AC=$\sqrt{17}$，BC=8，线段BC所在直线以每秒2个单位的速度沿BA方向运动，并始终保持与原位置平行．该直线与AB、AC分别交于点M、N，记x秒时，并设△AMN中MN边上的高为y．试写出y关于x的函数关系式y=-2x+$\sqrt{13}$，自变量x的取值范围是0＜x＜$\sqrt{13}$．
分析 过A作AH⊥BC于H，交MN于D，在Rt△ABH与Rt△ACH中，根据勾股定理得到AB2-BH2=AC2-CH2求得BH=6，得到AH=$\sqrt{A{B}^{2}-B{H}^{2}}$=$\sqrt{13}$，根据线段的和差即可得到结论．
解答 
解：过A作AH⊥BC于H，交MN于D，
在Rt△ABH与Rt△ACH中，
AB2-BH2=AC2-CH2，
即72-BH2=（$\sqrt{17}$）2-（8-BH）2，
∴BH=6，
∴AH=$\sqrt{A{B}^{2}-B{H}^{2}}$=$\sqrt{13}$，
∴DH=2x，
∴y=$\sqrt{13}$-2x，（0＜x＜$\sqrt{13}$）．
故答案为：y=$\sqrt{13}$-2x，（0＜x＜$\sqrt{13}$）．
点评 此题考查了相似三角形的判定与性质，勾股定理，过A作AH⊥BC于H构造直角三角形是解此题的关键．
练习册系列答案
相关题目
