题目内容
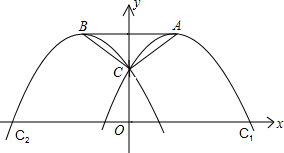 已知抛物线C1:y=-x2+2mx+1(m为常数,且m>0)的顶点为A,与y轴交于点C;抛物线C2与抛物线C1关于y轴对称,其顶点为B,连接AC,BC,AB.
已知抛物线C1:y=-x2+2mx+1(m为常数,且m>0)的顶点为A,与y轴交于点C;抛物线C2与抛物线C1关于y轴对称,其顶点为B,连接AC,BC,AB.(1)当m=1时,判定△ABC的形状,并说明理由;
(2)抛物线C1上是否存在点P,使得四边形ABCP为菱形?如果存在,请求出m的值;如果不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)根据轴对称的性质可得:AC=BC等腰三角形,借助于辅助线,又可求得∠ACy=45°,可得△ABC为等腰直角三角形;
(2)首先假设成立,根据菱形的性质求解,求得m=
,所以存在.
(2)首先假设成立,根据菱形的性质求解,求得m=
| 3 |
解答:解:(1)当m=1时,△ABC为等腰直角三角形. 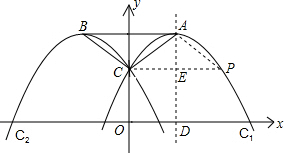
理由如下:
如图:∵点A与点B关于y轴对称,点C又在y轴上,
∴AC=BC.
过点A作抛物线C1的对称轴,交x轴于D,过点C作CE⊥AD于E.
当m=1时,顶点A的坐标为A(1,2),
∴CE=1.
又∵点C的坐标为(0,1),AE=2-1.
∴AE=CE.从而∠ECA=45°,
∴∠ACy=45°.
由对称性知∠BCy=∠ACy=45°,
∴∠ACB=90°.
∴△ABC为等腰直角三角形.
(2)假设抛物线C1上存在点P,使得四边形ABCP为菱形,则PC=AB=BC.
由(1)知,AC=BC,
∴AB=BC=AC.
∴△ABC为等边三角形.
∴∠ACy=∠BCy=30°.
∵四边形ABCP为菱形,且点P在C1上,
∴点P与点C关于AD对称.
∴PC与AD的交点也为点E,
因此∠ACE=90°-30°=60°.
∵点A,C的坐标分别为A(m,m2+1),C(0,1),
∴AE=m2+1-1=m2,CE=m.
在Rt△ACE中,tan60°=
=
=
.
∴m=±
,
∵m>0,
∴m=
,
故抛物线C1上存在点P,使得四边形ABCP为菱形,
此时m=
.

理由如下:
如图:∵点A与点B关于y轴对称,点C又在y轴上,
∴AC=BC.
过点A作抛物线C1的对称轴,交x轴于D,过点C作CE⊥AD于E.
当m=1时,顶点A的坐标为A(1,2),
∴CE=1.
又∵点C的坐标为(0,1),AE=2-1.
∴AE=CE.从而∠ECA=45°,
∴∠ACy=45°.
由对称性知∠BCy=∠ACy=45°,
∴∠ACB=90°.
∴△ABC为等腰直角三角形.
(2)假设抛物线C1上存在点P,使得四边形ABCP为菱形,则PC=AB=BC.
由(1)知,AC=BC,
∴AB=BC=AC.
∴△ABC为等边三角形.
∴∠ACy=∠BCy=30°.
∵四边形ABCP为菱形,且点P在C1上,
∴点P与点C关于AD对称.
∴PC与AD的交点也为点E,
因此∠ACE=90°-30°=60°.
∵点A,C的坐标分别为A(m,m2+1),C(0,1),
∴AE=m2+1-1=m2,CE=m.
在Rt△ACE中,tan60°=
| AE |
| CE |
| m2 |
| m |
| 3 |
∴m=±
| 3 |
∵m>0,
∴m=
| 3 |
故抛物线C1上存在点P,使得四边形ABCP为菱形,
此时m=
| 3 |
点评:此题考查了二次函数与四边形以及轴对称图形的综合知识,解题时要注意辅助线选择与应用,还要注意数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列说法不正确的是( )
| A、了解一批电视机的使用寿命适合用抽样调查 | ||||
| B、“彩票中奖的概率为0.1%”表示买1000张彩票肯定会中奖 | ||||
C、“抛一枚均匀的正方体般子,朝上的点数是2的概率
| ||||
| D、在一个装有白球和绿球的袋中摸球,摸出黑球是不可能事件 |
下列结论正确的是( )
| A、a2b3c是五次单项式 |
| B、xyz的系数是0 |
| C、x5+3x2y4-27是六次三项式 |
| D、3x2-x+1的一次项系数是1 |
方程2|x|+
=0的解是( )
| |y| |
| 3 |
A、
| |||||
B、
| |||||
C、
| |||||
D、
|

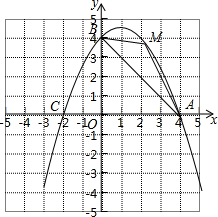 如图,在平面直角坐标系中,已知抛物线经过点A(4,0),B(0,4),C(-2,0)三点.
如图,在平面直角坐标系中,已知抛物线经过点A(4,0),B(0,4),C(-2,0)三点.