题目内容
 如图,直线y=-2x+2与x轴、y轴分别相交于点A和B.
如图,直线y=-2x+2与x轴、y轴分别相交于点A和B.(1)直接写出坐标:点A
(2)以线段AB为一边在第一象限内作?ABCD,其顶点D(3,1)在双曲线y=
| k |
| x |
①求证:四边形ABCD是正方形;
②试探索:将正方形ABCD沿x轴向左平移多少个单位长度时,点C恰好落在双曲线y=
| k |
| x |
考点:反比例函数综合题
专题:
分析:(1)分别令x=0,求出y的值;令y=0,求出x的值即可得出点B与点A的坐标;
(2)①过点D作DE⊥x轴于点E,由全等三角形的性质可得出△AOB≌△DEA,故可得出AB=AD,再利用待定系数法求出直线AD的解析式即可得出AB⊥AD,由此可得出结论;
②过点C作CF⊥y轴,利用△AOB≌△DEA,同理可得出:△AOB≌△BFC,即可得出C点纵坐标,如果点在图象上,利用纵坐标求出横坐标即可.
(2)①过点D作DE⊥x轴于点E,由全等三角形的性质可得出△AOB≌△DEA,故可得出AB=AD,再利用待定系数法求出直线AD的解析式即可得出AB⊥AD,由此可得出结论;
②过点C作CF⊥y轴,利用△AOB≌△DEA,同理可得出:△AOB≌△BFC,即可得出C点纵坐标,如果点在图象上,利用纵坐标求出横坐标即可.
解答: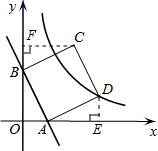 解:(1)∵令x=0,则y=2;令y=0,则x=1,
解:(1)∵令x=0,则y=2;令y=0,则x=1,
∴A(1,0),B(0,2).
故答案为:(1,0),(0,2);
(2)①过点D作DE⊥x轴于点E,
∵A(1,0),B(2,0),D(3,1),
∴AE=OB=2,OA=DE=1,
在△AOB与△DEA中,
,
∴△AOB≌△DEA(SAS),
∴AB=AD,
设直线AD的解析式为y=kx+b(k≠0),
∴
,
解得
,
∵(-2)×
=-1,
∴AB⊥AD,
∵四边形ABCD是正方形;
②过点C作CF⊥y轴,
∵△AOB≌△DEA,
∴同理可得出:△AOB≌△BFC,
∴OB=CF=2
∵C点纵坐标为:3,
代入y=
,
∴x=1,
∴应该将正方形ABCD沿X轴向左平移2-1=1个单位长度时,点C的对应点恰好落在(1)中的双曲线上.
 解:(1)∵令x=0,则y=2;令y=0,则x=1,
解:(1)∵令x=0,则y=2;令y=0,则x=1,∴A(1,0),B(0,2).
故答案为:(1,0),(0,2);
(2)①过点D作DE⊥x轴于点E,
∵A(1,0),B(2,0),D(3,1),
∴AE=OB=2,OA=DE=1,
在△AOB与△DEA中,
|
∴△AOB≌△DEA(SAS),
∴AB=AD,
设直线AD的解析式为y=kx+b(k≠0),
∴
|
解得
|
∵(-2)×
| 1 |
| 2 |
∴AB⊥AD,
∵四边形ABCD是正方形;
②过点C作CF⊥y轴,
∵△AOB≌△DEA,
∴同理可得出:△AOB≌△BFC,
∴OB=CF=2
∵C点纵坐标为:3,
代入y=
| 3 |
| x |
∴x=1,
∴应该将正方形ABCD沿X轴向左平移2-1=1个单位长度时,点C的对应点恰好落在(1)中的双曲线上.
点评:此题主要考查了反比例函数的综合题,根据图象上点的坐标性质以及全等三角形的判定与性质得出是解题关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
下列各组线段中,不能构成直角三角形的是( )
A、2、1、
| ||
B、5、5、5
| ||
| C、6、8、9 | ||
| D、3k、4k、5k(k>0) |
下列计算错误的是( )
A、3
| ||||||
| B、x2•x3=x6 | ||||||
| C、-2+|-2|=0 | ||||||
D、(-3)-2=
|
 如图,是某商场4种品牌的商品销售情况统计图,其中甲品牌所占的扇形的圆心角是( )
如图,是某商场4种品牌的商品销售情况统计图,其中甲品牌所占的扇形的圆心角是( )| A、36° | B、108° |
| C、72° | D、162° |
 如图,海中有一个小岛C,今有一货船由西向东航行,在A处测得小岛C在北偏东60°方向,货船向正东方向航行16海里到达B处,在B处测得小岛C在北偏东15°方向,求此时货船与小岛C的距离.(结果精确到0.01海里)(参考数据:
如图,海中有一个小岛C,今有一货船由西向东航行,在A处测得小岛C在北偏东60°方向,货船向正东方向航行16海里到达B处,在B处测得小岛C在北偏东15°方向,求此时货船与小岛C的距离.(结果精确到0.01海里)(参考数据: