题目内容
 如图,海中有一个小岛C,今有一货船由西向东航行,在A处测得小岛C在北偏东60°方向,货船向正东方向航行16海里到达B处,在B处测得小岛C在北偏东15°方向,求此时货船与小岛C的距离.(结果精确到0.01海里)(参考数据:
如图,海中有一个小岛C,今有一货船由西向东航行,在A处测得小岛C在北偏东60°方向,货船向正东方向航行16海里到达B处,在B处测得小岛C在北偏东15°方向,求此时货船与小岛C的距离.(结果精确到0.01海里)(参考数据:| 2 |
| 3 |
考点:解直角三角形的应用-方向角问题
专题:
分析:过点B作BE⊥AC于点E,在Rt△ABE中,∠CAB=30°,即可利用三角函数求得BE,再在Rt△BEC中利用三角函数即可求得BC的长.
解答: 解:过B作BE⊥AC于点E.
解:过B作BE⊥AC于点E.
由题意可知:∠BAC=30°,∠C=45°,BE=AB•sin∠BAC=16×
=8(海里),
∴CE=BE=8,
∴BC=8
≈8×1.414=11.31(海里).
答:此时货船与小岛C距离是11.31海里.
 解:过B作BE⊥AC于点E.
解:过B作BE⊥AC于点E.由题意可知:∠BAC=30°,∠C=45°,BE=AB•sin∠BAC=16×
| 1 |
| 2 |
∴CE=BE=8,
∴BC=8
| 2 |
答:此时货船与小岛C距离是11.31海里.
点评:本题主要考查了方向角的定义,解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
下列运算正确的是( )
| A、a3•a2=a5 |
| B、(a2)3=a5 |
| C、a3+a3=a6 |
| D、(a+b)2=a2+b2 |
下列函数
(1)y=πx;(2)y=2x-1;(3)y=
;(4)y=2-1-3x.
是一次函数的有( )
(1)y=πx;(2)y=2x-1;(3)y=
| 1 |
| x |
是一次函数的有( )
| A、4个 | B、3个 | C、2个 | D、1个 |
 如图,直线y=-2x+2与x轴、y轴分别相交于点A和B.
如图,直线y=-2x+2与x轴、y轴分别相交于点A和B.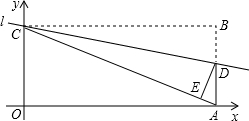 在直角坐标系中,四边形OABC为矩形,直线l:y=-
在直角坐标系中,四边形OABC为矩形,直线l:y=- 如图,一次函数y=-x+2的图象与反比例函数y=-
如图,一次函数y=-x+2的图象与反比例函数y=-