Question

14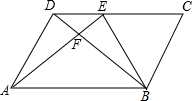．如图，在平行四边形ABCD中，DE：CE=2：3，则S_△DEF：S_△EFB：S_△FAB等于（　　）

• A． 4：10：25
• B． 4：9：25
• C． 2：3：25
• D． 2：5：25

Answer 1

分析 由DE：EC=2：3，四边形ABCD为平行四边形，得到DE：AB=2：5，又△DEF∽△FAB，得到DE：AB=DF：FB=2：5，根据等高两三角形面积的比等于底边的比，得出S_△DEF：S_△EFB=DF：FB=2：5；根据相似三角形面积的比等于相似比的平方得到S_△DEF：S_△FAB=2²：5²=4：25，最后得到S_△DEF：S_△EFB：S_△FAB的比值．

解答 解：∵DE：CE=2：3，
∴DE：DC=2：5，
又∵四边形ABCD为平行四边形，
∴AB=DC，
∴DE：AB=2：5，
∵DE∥AB，
∴△DEF∽△FAB，
∴DE：AB=DF：FB=2：5，
∴S_△DEF：S_△EFB=DF：FB=2：5，
S_△DEF：S_△FAB=2²：5²=4：25，
∴S_△DEF：S_△EFB：S_△FAB=4：10：25．
故选A．

点评 本题考查了平行四边形的性质、相似三角形的判定与性质；熟练掌握平行四边形的性质，并能进行推理论证与计算是解决问题的关键．