题目内容
8.已知平行四边形ABCD中,对角线AC⊥AB,AB:BC=3:5,AC=8,求平行四边形ABCD的面积.分析 先根据勾股定理求出BC的长,再由三角形的面积公式解答即可.
解答  解:∵对角线AC⊥AB,
解:∵对角线AC⊥AB,
∴∠ACB=90°,
∴AB2=AC2+BC2,
∵AB:BC=3:5,AC=8,
∴AB=10,BC=6,
∴平行四边形ABCD的面积=BC•AC=48.
点评 本题考查了平行四边形的对边相等的性质和勾股定理,求出BC的长是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.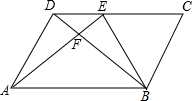 如图,在平行四边形ABCD中,DE:CE=2:3,则S△DEF:S△EFB:S△FAB等于( )
如图,在平行四边形ABCD中,DE:CE=2:3,则S△DEF:S△EFB:S△FAB等于( )
 如图,在平行四边形ABCD中,DE:CE=2:3,则S△DEF:S△EFB:S△FAB等于( )
如图,在平行四边形ABCD中,DE:CE=2:3,则S△DEF:S△EFB:S△FAB等于( )| A. | 4:10:25 | B. | 4:9:25 | C. | 2:3:25 | D. | 2:5:25 |
17.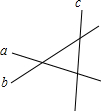 如图,直线a、b、c表示三条互相交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
如图,直线a、b、c表示三条互相交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
 如图,直线a、b、c表示三条互相交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
如图,直线a、b、c表示三条互相交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )| A. | 1处 | B. | 2处 | C. | 3处 | D. | 4处 |
18.有一个三角形的两边长分别为4和7,第三边的长是方程(x-5)(x-12)=0的根,则这个三角形的周长为( )
| A. | 16 | B. | 23 | C. | 24 | D. | 16或23 |
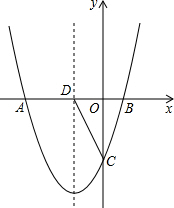 如图,抛物线y1=$\frac{1}{2}$x2+bx+c与x轴交于点A、B,交y轴于点C(0,-2$\sqrt{3}$),且抛物线对称轴x=-2交x轴于点D,E是抛物线在第3象限内一动点.
如图,抛物线y1=$\frac{1}{2}$x2+bx+c与x轴交于点A、B,交y轴于点C(0,-2$\sqrt{3}$),且抛物线对称轴x=-2交x轴于点D,E是抛物线在第3象限内一动点. 如图,正方形ABCD的面积为256,点F在AD上,点E在AB的延长线上,直角△CEF的面积为200,则BE的值为12.
如图,正方形ABCD的面积为256,点F在AD上,点E在AB的延长线上,直角△CEF的面积为200,则BE的值为12.