题目内容
11.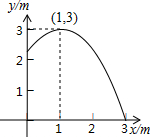 如图,池中心竖直水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管的长为( )
如图,池中心竖直水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管的长为( )| A. | 2.1m | B. | 2.2m | C. | 2.3m | D. | 2.25m |
分析 设抛物线的解析式为y=a(x-1)2+3(0≤x≤3),将(3,0)代入求得a值,则x=0时得的y值即为水管的长.
解答 解:由于在距池中心的水平距离为1m时达到最高,高度为3m,
则设抛物线的解析式为:
y=a(x-1)2+3(0≤x≤3),
代入(3,0)求得:a=$\frac{3}{4}$.
将a值代入得到抛物线的解析式为:
y=-$\frac{3}{4}$(x-1)2+3(0≤x≤3),
令x=0,则y=$\frac{9}{4}$=2.25.
则水管长为2.25m,
故选:D.
点评 本题考查了二次函数在实际生活中的运用,重点是二次函数解析式的求法,利用顶点式求出解析式是解题关键.

练习册系列答案
相关题目
1.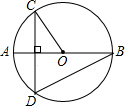 如图,线段AB是⊙O的直径,弦CD⊥AB,∠OCD=40°,则∠ABD的度数是( )
如图,线段AB是⊙O的直径,弦CD⊥AB,∠OCD=40°,则∠ABD的度数是( )
 如图,线段AB是⊙O的直径,弦CD⊥AB,∠OCD=40°,则∠ABD的度数是( )
如图,线段AB是⊙O的直径,弦CD⊥AB,∠OCD=40°,则∠ABD的度数是( )| A. | 20° | B. | 25° | C. | 30° | D. | 40° |
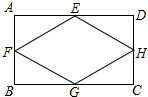 如图,E、F、G、H分别为矩形ABCD四边的中点.
如图,E、F、G、H分别为矩形ABCD四边的中点. 如图,△ABC中,∠C=90°,AD平分∠BAC,AB=7,CD=2,则△ABD的面积是7.
如图,△ABC中,∠C=90°,AD平分∠BAC,AB=7,CD=2,则△ABD的面积是7. 如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.
如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.