题目内容
4. 如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.
如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.(1)求证:DE是⊙O的切线;
(2)若△ABC的边长为4,求EF的长度.
分析 (1)连接OD,根据等边三角形的性质求出∠ODE=90°,根据切线的判定定理证明即可;
(2)连接AD,BF,根据等边三角形的性质求出DC、CF,根据直角三角形的性质求出EC,结合图形计算即可.
解答 (1)证明:如图1,连接OD,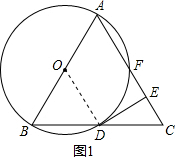
∵△ABC是等边三角形,
∴∠B=∠C=60°.
∵OB=OD,
∴∠ODB=∠B=60°.
∵DE⊥AC,
∴∠DEC=90°.
∴∠EDC=30°.
∴∠ODE=90°.
∴DE⊥OD于点D.
∵点D在⊙O上,
∴DE是⊙O的切线;
(2)解:如图2,连接AD,BF,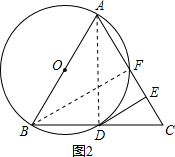
∵AB为⊙O直径,
∴∠AFB=∠ADB=90°.
∴AF⊥BF,AD⊥BD.
∵△ABC是等边三角形,
∴$DC=\frac{1}{2}BC=2$,$FC=\frac{1}{2}AC=2$.
∵∠EDC=30°,
∴$EC=\frac{1}{2}DC=1$.
∴FE=FC-EC=1.
点评 本题考查的是切线的判定、等边三角形的性质以及直角三角形的性质,掌握经过半径的外端且垂直于这条半径的直线是圆的切线是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
12. 将一副三角尺按如图方式进行摆放,则∠1的度数为( )
将一副三角尺按如图方式进行摆放,则∠1的度数为( )
 将一副三角尺按如图方式进行摆放,则∠1的度数为( )
将一副三角尺按如图方式进行摆放,则∠1的度数为( )| A. | 60° | B. | 90° | C. | 120° | D. | 135° |
19. 如图,点D,E分别在△ABC的AB,AC边上,增加下列条件中的一个:①∠AED=∠B,②∠ADE=∠C,③$\frac{AE}{AB}=\frac{DE}{BC}$,④$\frac{AD}{AC}=\frac{AE}{AB}$,⑤AC2=AD•AE,使△ADE与△ACB一定相似的有( )
如图,点D,E分别在△ABC的AB,AC边上,增加下列条件中的一个:①∠AED=∠B,②∠ADE=∠C,③$\frac{AE}{AB}=\frac{DE}{BC}$,④$\frac{AD}{AC}=\frac{AE}{AB}$,⑤AC2=AD•AE,使△ADE与△ACB一定相似的有( )
 如图,点D,E分别在△ABC的AB,AC边上,增加下列条件中的一个:①∠AED=∠B,②∠ADE=∠C,③$\frac{AE}{AB}=\frac{DE}{BC}$,④$\frac{AD}{AC}=\frac{AE}{AB}$,⑤AC2=AD•AE,使△ADE与△ACB一定相似的有( )
如图,点D,E分别在△ABC的AB,AC边上,增加下列条件中的一个:①∠AED=∠B,②∠ADE=∠C,③$\frac{AE}{AB}=\frac{DE}{BC}$,④$\frac{AD}{AC}=\frac{AE}{AB}$,⑤AC2=AD•AE,使△ADE与△ACB一定相似的有( )| A. | ①②④ | B. | ②④⑤ | C. | ①②③④ | D. | ①②③⑤ |
9.顺次连接四边形的各边中点得到的四边形是正方形,则这个四边形对角线应满足( )
| A. | 相等、平分且垂直 | B. | 相等且平分 | C. | 相等且垂直 | D. | 垂直且平分 |
13. 二次函数y=-x2-6x-2的图象如图所示,若点A(1,y1),B(2,y2)是图象上的两点,则y1与y2的大小关系是( )
二次函数y=-x2-6x-2的图象如图所示,若点A(1,y1),B(2,y2)是图象上的两点,则y1与y2的大小关系是( )
 二次函数y=-x2-6x-2的图象如图所示,若点A(1,y1),B(2,y2)是图象上的两点,则y1与y2的大小关系是( )
二次函数y=-x2-6x-2的图象如图所示,若点A(1,y1),B(2,y2)是图象上的两点,则y1与y2的大小关系是( )| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 不能确定 |
 观察如图,A点为正比例函数y=$\frac{3}{4}$x与一次函数y=-x+7的图象的交点
观察如图,A点为正比例函数y=$\frac{3}{4}$x与一次函数y=-x+7的图象的交点