题目内容
4．一个直角三角形的两条直角边长为6和8，则它的斜边上的高是4.8．分析 首先根据题意求出斜边的长，再根据三角形的面积公式即可求出斜边上的高．
解答 解：∵直角三角形的两直角边长为6和8，
斜边长为：$\sqrt{{6}^{2}+{8}^{2}}$=10，
三角形的面积=$\frac{1}{2}$×6×8=24，
设斜边上的高为x，则
$\frac{1}{2}$x•10=24，
解得x=4.8．
故答案为：4.8．
点评 此题主要考查了勾股定理，以及三角形的面积公式，解决问题的关键是掌握直角三角形的面积公式的两种计算方法．
练习册系列答案
相关题目
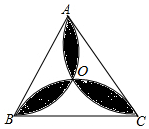如图，在边长为a的等边三角形ABC中有一个由三个全等的叶形所组成的“三叶草”图形，点O是△ABC的外心，则该“三叶草”图形的面积是$\frac{π}{3}$a2-$\frac{\sqrt{3}}{2}$a2．
15．某个三角形的三边长有可能是（ ）
| A． | 20，16，2016 | B． | 2，2，4 | C． | 2，2，2 | D． | 1，2，4 |
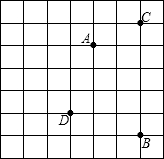如图，大正方形是由边长为1的小正方形拼成的，A，B，C，D四个点是小正方形的顶点，以其中三个点为顶点，可以构成直角三角形的个数是（ ）
