题目内容
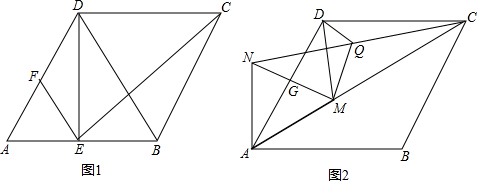
16.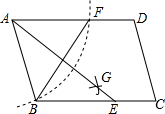 如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=4,则AE的长为( )
如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=4,则AE的长为( )| A. | $\sqrt{7}$ | B. | 2$\sqrt{7}$ | C. | 3$\sqrt{7}$ | D. | 4$\sqrt{7}$ |
分析 由基本作图得到AB=AF,加上AO平分∠BAD,则根据等腰三角形的性质得到AO⊥BF,BO=FO=$\frac{1}{2}$BF=3,再根据平行四边形的性质得AF∥BE,得出∠1=∠3,于是得到∠2=∠3,根据等腰三角形的判定得AB=EB,然后再根据等腰三角形的性质得到AO=OE,最后利用勾股定理计算出AO,从而得到AE的长.
解答 解:连结EF,AE与BF交于点O,如图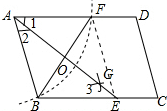
∵AB=AF,AO平分∠BAD,
∴AO⊥BF,BO=FO=$\frac{1}{2}$BF=3,
∵四边形ABCD为平行四边形,
∴AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=EB,
∵BO⊥AE,
∴AO=OE,
在Rt△AOB中,AO=$\sqrt{A{B}^{2}-O{B}^{2}}$=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$,
∴AE=2AO=2$\sqrt{7}$.
故选B.
点评 本题考查的是作图-基本作图、平行四边形的性质、勾股定理、平行线的性质、等腰三角形的判定;熟练掌握平行四边形的性质,由勾股定理求出AO是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
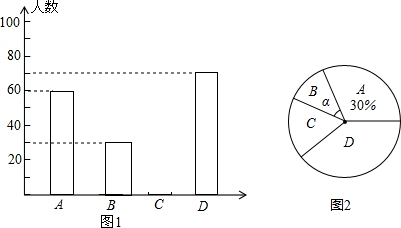
8. 请根据下列图表信息解答问题:
请根据下列图表信息解答问题:
(1)表中空缺的数据为9%;(精确到1%)
(2)求统计表中增长率的平均数及中位数;
(3)预测2017年的观影人次,并说明理由.
 请根据下列图表信息解答问题:
请根据下列图表信息解答问题:| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 年增长率 | 31% | 27% | 32% | 35% | 52% |
(2)求统计表中增长率的平均数及中位数;
(3)预测2017年的观影人次,并说明理由.
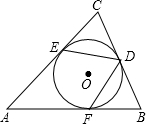 如图,已知⊙O内切于△ABC,切点分别为D、E、F,若∠A=50°,则∠EDF=65°.
如图,已知⊙O内切于△ABC,切点分别为D、E、F,若∠A=50°,则∠EDF=65°.
 如图,直线L1∥L2,且分别与△ABC的两边AB、AC相交,若∠A=40°,∠1=45°,则∠2的度数为95°.
如图,直线L1∥L2,且分别与△ABC的两边AB、AC相交,若∠A=40°,∠1=45°,则∠2的度数为95°.