题目内容
20.直角三角形ABCD中,∠BAC=90°,AB=AC=1,以AC为一边在△ABC外部作等腰直角三角形ACD,则线段BD的长为2或$\sqrt{5}$或$\frac{\sqrt{10}}{2}$.分析 分情况讨论,①以A为直角顶点,向外作等腰直角三角形DAC;
②以C为直角顶点,向外作等腰直角三角形ACD;
③以AC为斜边,向外作等腰直角三角形ADC.分别画图,并求出BD.
解答 解:①以A为直角顶点,向外作等腰直角三角形DAC,
∵∠DAC=90°,且AD=AC,
∴BD=BA+AD=1+1=2;
②以C为直角顶点,向外作等腰直角三角形ACD,
连接BD,过点D作DE⊥BC,交BC的延长线于E.
∵△ABC是等腰直角三角形,∠ACD=90°,
∴∠DCE=45°,
又∵DE⊥CE,
∴∠DEC=90°,
∴∠CDE=45°,
∴CE=DE=1×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{2}$,
在Rt△BAC中,BC=$\sqrt{2}$,
∴BD=$\sqrt{B{E}^{2}+D{E}^{2}}$=$\sqrt{5}$;
③以AC为斜边,向外作等腰直角三角形ADC,
∵∠ADC=90°,AD=DC,且AC=2,
∴AD=DC=ACsin45°=1×$\frac{\sqrt{2}}{2}$,
又∵△ABC、△ADC是等腰直角三角形,
∴∠ACB=∠ACD=45°,
∴∠BCD=90°,
又∵在Rt△ABC中,BC=$\sqrt{2}$,
∴BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=$\frac{\sqrt{10}}{2}$,
综上所述:BD的长等于2或$\sqrt{5}$或$\frac{\sqrt{10}}{2}$.
故答案是:2或$\sqrt{5}$或$\frac{\sqrt{10}}{2}$.
点评 本题考查了等腰直角三角形的性质、勾股定理等知识,解题时注意分类讨论,不要漏掉所有可能的情况.

练习册系列答案
相关题目
11.四边形ABCD中,对角线AC与BD交于点O,下列条件中不一定能判定这个四边形是平行四边形的是( )
| A. | AB=DC,∠ABC=∠ADC | B. | AD∥BC,AB∥DC | C. | AB=DC,AD=BC | D. | OA=OC,OB=OD |
15.若顺次连接一个四边形的各边的中点所得的四边形是矩形,则原来的四边形的两条对角线( )
| A. | 互相垂直且相等 | B. | 相等 | C. | 互相平分且相等 | D. | 互相垂直 |
 如图所示,请写出一个能判定l1∥l2的条件:∠1=∠3或∠4=∠5或∠2+∠4=180°.
如图所示,请写出一个能判定l1∥l2的条件:∠1=∠3或∠4=∠5或∠2+∠4=180°.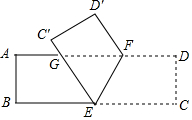 如图,将一张长方形纸片ABCD沿EF折叠,使顶点C、D分别落在C′、D′处,C′E交AF于点G,若∠CEF=65°,则∠GFD′=50°.
如图,将一张长方形纸片ABCD沿EF折叠,使顶点C、D分别落在C′、D′处,C′E交AF于点G,若∠CEF=65°,则∠GFD′=50°.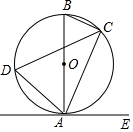 如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.