题目内容
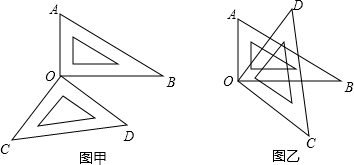
将两个三角尺如图甲摆放,问:
(1)①∠AOD和∠BOC相等吗?说明理由.
②∠AOC和∠BOD在数量上有何关系?
(2)若将等腰的三角尺绕点O旋转到如图乙的位置,∠AOD和∠BOC相等吗?说明理由.
(1)①∠AOD和∠BOC相等吗?说明理由.
②∠AOC和∠BOD在数量上有何关系?
(2)若将等腰的三角尺绕点O旋转到如图乙的位置,∠AOD和∠BOC相等吗?说明理由.

考点:余角和补角
专题:
分析:(1)根据直角三角板可得:∠AOB=∠COD=90°,再根据等式的性质两边同时加上∠BOD可得∠AOD=∠COB;根据周角为360°,可得∠AOC和∠BOD互补;
(2)根据直角三角板可得:∠AOB=∠COD=90°,再根据等式的性质两边同时减去∠BOD可得∠AOD=∠COB;根据角的和差关系可得∠BOD+∠AOC=∠BOD+∠AOB+∠COB进而可得∠BOD+∠AOC=180°.
(2)根据直角三角板可得:∠AOB=∠COD=90°,再根据等式的性质两边同时减去∠BOD可得∠AOD=∠COB;根据角的和差关系可得∠BOD+∠AOC=∠BOD+∠AOB+∠COB进而可得∠BOD+∠AOC=180°.
解答:解:(1)①∠AOD和∠BOC相等,②∠AOC和∠BOD互补;
理由:∵∠AOB=∠COD=90°,
∴∠AOB+∠BOD=∠COD+∠BOD,
∴∠AOD=∠COB;
∵∠AOB=∠COD=90°,
∴∠BOD+∠AOC=360°-90°-90°=180°,
∴∠AOC和∠BOD互补;
(2)成立;
理由:∵∠AOB=∠COD=90°,
∴∠AOB-∠BOD=∠COD-∠BOD,
∴∠AOD=∠COB;
∵∠AOB=∠COD=90°,
∴∠BOD+∠AOC=∠BOD+∠AOB+∠COB=90°+∠BOD+∠COB=90°+∠DOC=90°+90°=180°.

理由:∵∠AOB=∠COD=90°,
∴∠AOB+∠BOD=∠COD+∠BOD,
∴∠AOD=∠COB;
∵∠AOB=∠COD=90°,
∴∠BOD+∠AOC=360°-90°-90°=180°,
∴∠AOC和∠BOD互补;
(2)成立;
理由:∵∠AOB=∠COD=90°,
∴∠AOB-∠BOD=∠COD-∠BOD,
∴∠AOD=∠COB;
∵∠AOB=∠COD=90°,
∴∠BOD+∠AOC=∠BOD+∠AOB+∠COB=90°+∠BOD+∠COB=90°+∠DOC=90°+90°=180°.
点评:此题主要考查了余角和补角,关键是正确分清图中角之间的和差关系.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
下列说法中不正确的是( )
| A、-3.14既是负数,分数,也是有理数 |
| B、0既不是正数,也不是负数,但是整数 |
| C、-2000既是负数,也是整数,但不是有理数 |
| D、O是正数和负数的分界 |
 如图,线段AC、BD为四边形ABCD对角线.已知,∠ABC=∠ADC=90°,AD=DC,tan∠ACB=
如图,线段AC、BD为四边形ABCD对角线.已知,∠ABC=∠ADC=90°,AD=DC,tan∠ACB= 从图中能数出
从图中能数出 一张长方形纸长26厘米,宽19厘米,将这张纸四角沿图中虚线对折,那么四条虚线所围成的正方形的面积是多少?
一张长方形纸长26厘米,宽19厘米,将这张纸四角沿图中虚线对折,那么四条虚线所围成的正方形的面积是多少? 如图,∠CAB=∠DBA,AC=BD,说明下列结果成立的理由.
如图,∠CAB=∠DBA,AC=BD,说明下列结果成立的理由.