题目内容
19. 已知二次函数y=ax2+bx+c的图象与坐标轴交于A、B、C三点,点A的坐标为(-1,0),点 C的坐标为 (0,3),对称轴是x=1.
已知二次函数y=ax2+bx+c的图象与坐标轴交于A、B、C三点,点A的坐标为(-1,0),点 C的坐标为 (0,3),对称轴是x=1.(1)求这个二次函数的解析式;
(2)过顶点M和点C的直线y=kx+g与x轴交于点D,求点D的坐标;
(3)在二次函数的图象上是否存在点N,与A、C、D三点构成一个平行四边形?若存在,写出点N的坐标;否则写出理由.
分析 (1)根据对称轴和A的坐标求得B的坐标,然后根据勾股定理即可求得抛物线的解析式;
(2)根据二次函数的解析式求得顶点M的坐标,根据待定系数法求得直线的解析式,然后令y=0,即可求得D点的坐标;
(3)求得C点的对称点N的坐标,然后得到CN∥AD,且CN=AD,即可证得四边形ADCN是平行四边形,即可得出在二次函数的图象上是否存在点N,与A、C、D三点构成一个平行四边形.
解答 解:(1)∵点A的坐标为(-1,0),对称轴是x=1.
∴抛物线与x轴的另一个交点B(3,0),
设抛物线的解析式为y=a(x+1)(x-3),
∵点 C(0,3)在抛物线上,
∴3=-3a,
解得a=-1,
∴y=-(x+1)(x-3)=-x2+2x+3,
∴这个二次函数的解析式为y=-x2+2x+3;
(2)∵y=-x2+2x+3=-(x-1)2+4,
∴M(1,4),
∵C(0,3),
∴$\left\{\begin{array}{l}{k+g=4}\\{g=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{g=3}\end{array}\right.$,
∴直线y=kx+g的解析式为y=x+3,
令y=0,求得x=-3,
∴D(-3,0);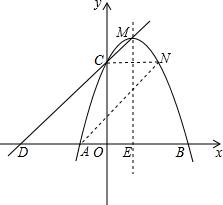
(3)存在,
如图,把y=3代入y=-x2+2x+3得-x2+2x+3=3,
解得x1=0,x2=2,
∴点C的对称点N的坐标为(2,3),
∵CN=2,AD=3-1=2,
∴CN=AD,
∵CN∥x轴,
∴CN∥AD,
∴四边形ADCN是平行四边形,
∴在二次函数的图象上是否存在点N,与A、C、D三点构成一个平行四边形,此时N(2,3).
点评 本题主要考查了二次函数的交点式、抛物线的对称性、平行四边形的判定与性质,解一元二次方程等知识点,熟练掌握待定系数法求函数的解析式以及数形结合思想的运用是解答此题的关键.

| 转让数量(套) | 1200 | 1100 | 1000 | 900 | 800 | 700 | 600 | 500 | 400 | 300 | 200 | 100 |
| 价格(元/套) | 240 | 250 | 260 | 270 | 280 | 290 | 300 | 310 | 320 | 330 | 340 | 350 |
(2)现在经销商甲面临三种选择:
方案1:不转让A品牌服装,也不经销B品牌服装;
方案2:全部转让A品牌服装,用转让来的资金购B品牌服装,经销B品牌服装;
方案3:部分转让A品牌服装,用转让来的资金购B品牌服装,经销B品牌服装,同时也经销A品牌服装.
如果你是经销商甲,为使自己在服装经销过程中获得最大利润,你选择哪一种方案?怎样选择?为什么?
 如图,BC是⊙O直径,A是圆周上一点,把△ABC绕点C顺时针旋转得△EDC,连结BD,当BD∥AC时,记旋转角为x度,若∠ABC=y度,则y与x之间满足的函数关系式为( )
如图,BC是⊙O直径,A是圆周上一点,把△ABC绕点C顺时针旋转得△EDC,连结BD,当BD∥AC时,记旋转角为x度,若∠ABC=y度,则y与x之间满足的函数关系式为( )| A. | y=180-2x | B. | y=$\frac{1}{2}$x+90 | C. | y=2x | D. | y=$\frac{1}{2}$x |
 如图,⊙O的半径为10,点C为$\widehat{AB}$ 的中点,过点C作弦CD∥OA,交OB于E.
如图,⊙O的半径为10,点C为$\widehat{AB}$ 的中点,过点C作弦CD∥OA,交OB于E.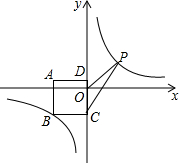 如图,正方形ABCD在平面直角坐标系中,且AD∥x轴,点A的坐标为(-4,1),点D的坐标为(0,1),点B,P都在反比例函数y=$\frac{k}{x}$的图象上,且P时动点,连接OP,CP.
如图,正方形ABCD在平面直角坐标系中,且AD∥x轴,点A的坐标为(-4,1),点D的坐标为(0,1),点B,P都在反比例函数y=$\frac{k}{x}$的图象上,且P时动点,连接OP,CP.