题目内容
9.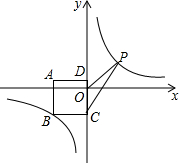 如图,正方形ABCD在平面直角坐标系中,且AD∥x轴,点A的坐标为(-4,1),点D的坐标为(0,1),点B,P都在反比例函数y=$\frac{k}{x}$的图象上,且P时动点,连接OP,CP.
如图,正方形ABCD在平面直角坐标系中,且AD∥x轴,点A的坐标为(-4,1),点D的坐标为(0,1),点B,P都在反比例函数y=$\frac{k}{x}$的图象上,且P时动点,连接OP,CP.(1)求反比例函数y=$\frac{k}{x}$的函数表达式;
(2)当点P的纵坐标为$\frac{9}{8}$时,判断△OCP的面积与正方形ABCD的面积的大小关系.
分析 (1)只需根据条件求出点B的坐标,然后运用待定系数法就可解决问题;
(2)易求出OC的长,然后只需根据条件求出点P的横坐标,就可求出△OCP的面积,然后再求出正方形ABCD的面积,就可解决问题.
解答 解:(1)∵四边形ABCD是正方形,A(-4,1),D(0,1),
∴OD=1,BC=DC=AD=4,
∴OC=3,
∴点B的坐标为(-4,-3).
∵点B在反比例函数y=$\frac{k}{x}$的图象上,
∴k=-4×(-3)=12,
∴反比例函数的表达式为y=$\frac{12}{x}$;
(2)∵点P在反比例函数y=$\frac{12}{x}$的图象上,点P的纵坐标为$\frac{9}{8}$,
∴点P的横坐标为$\frac{32}{3}$,
∴S△OCP=$\frac{1}{2}$×3×$\frac{32}{3}$=16.
∵S正方形ABCD=16,
∴△OCP的面积与正方形ABCD的面积相等.
点评 本题主要考查正方形的性质、运用待定系数法求反比例函数的表达式、反比例函数图象上点的坐标特征等知识,运用待定系数法是求函数解析式常用的方法,应熟练掌握.

练习册系列答案
相关题目
17.10月26日,眉山市2东坡区实验中学全体师生在操场隆重集会,举行“2015年读书月活动”.张萌调查了她所在班级5名同学一周内的累计读书时间,分别为:40分钟、45分钟、50分钟、40分钟、60分钟,则该组数据的平均数、中位数分别是( )
| A. | 47,45 | B. | 45,45 | C. | 40,45 | D. | 47,45 |
4.现有五张分别画有等边三角形、平行四边形、矩形、正五边形和圆的五个图形的卡片,它们的背面相同,小梅将它们的背面朝上,从中任意抽出一张,下列说法中正确的是( )
| A. | “抽出的图形是中心对称图形”属于必然事件 | |
| B. | “抽出的图形是六边形”属于随机事件 | |
| C. | 抽出的图形为四边形的概率是$\frac{2}{5}$ | |
| D. | 抽出的图形为轴对称图形的概率是$\frac{3}{5}$ |
18.计算-22-(-2)3×(-1)2-(-1)3的结果为( )
| A. | 5 | B. | -1 | C. | 24 | D. | -30 |
 已知二次函数y=ax2+bx+c的图象与坐标轴交于A、B、C三点,点A的坐标为(-1,0),点 C的坐标为 (0,3),对称轴是x=1.
已知二次函数y=ax2+bx+c的图象与坐标轴交于A、B、C三点,点A的坐标为(-1,0),点 C的坐标为 (0,3),对称轴是x=1. 如图,在△ABC中,AB=BC,∠ABC=100°,边BA绕点B顺时针旋转m°,(0<m<180)得到线段BD,连接AD、DC,若△ADC为等腰三角形,则m所有可能的取值是130或100或160.
如图,在△ABC中,AB=BC,∠ABC=100°,边BA绕点B顺时针旋转m°,(0<m<180)得到线段BD,连接AD、DC,若△ADC为等腰三角形,则m所有可能的取值是130或100或160.