题目内容
19．时钟上的分针和时针像两个运动员，绕眷它们的跑道昼夜不停地一直向前转．分针每小时转了360度，即每分钟转了6度，时针的速度是分针速度的$\frac{1}{12}$，即每分钟转了$\frac{1}{2}$度．你能进一步探索它们的运动规律，提出一些需应用一元一次方程解决的问题吗？分析 利用时针和分针的运动规律可求出它们在2点和3点之间相遇的时间，设此时相遇的时间为2点x分钟，则分针转6x度，时针转0.5x度，根据它们相差30度列方程30+0.5x=6x，然后解方程即可．
解答 解：利用时针和分针的运动规律可求出它们在2点和3点之间相遇的时间．
设此时相遇的时间为2点x分钟，
根据题意得30+0.5x=6x，解得x=5$\frac{5}{11}$，
所以在2点5$\frac{5}{11}$分钟时针与分针相遇．
点评 本题考查了一元一次方程的应用：首先审题找出题中的未知量和所有的已知量，直接设要求的未知量或间接设一关键的未知量为x，然后用含x的式子表示相关的量，找出之间的相等关系列方程、求解、作答，即设、列、解、答．设计一个追及问题，利用时针和分针所转角度列方程．
练习册系列答案
相关题目
9．
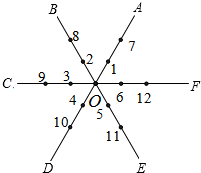如图，平面内有公共端点的六条射线OA，OB，OC，OD，OE，OF，从射线OA开始按逆时针方向依次在射线上写出数字1，2，3，4，5，6，7，…，则数字“2016”在（ ）
如图，平面内有公共端点的六条射线OA，OB，OC，OD，OE，OF，从射线OA开始按逆时针方向依次在射线上写出数字1，2，3，4，5，6，7，…，则数字“2016”在（ ）| A． | 射线OA上 | B． | 射线OB上 | C． | 射线OD上 | D． | 射线OF上 |
4．已知△ABC∽△A′B′C′，$\frac{AB}{A′B′}$=$\frac{2}{3}$，AB边上的中线CD=4cm，则A′B′边上的中线C′D′为（ ）
| A． | 6cm | B． | $\frac{8}{3}$cm | C． | 8cm | D． | 12cm |
8．等式$\sqrt{{a}^{2}}$=（$\sqrt{a}$）2成立的条件是（ ）
| A． | a是任意实数 | B． | a＞0 | C． | a＜0 | D． | a≥0 |
已知二次函数y=ax2+bx+c的图象与坐标轴交于A、B、C三点，点A的坐标为（-1，0），点 C的坐标为 （0，3），对称轴是x=1．