题目内容
如图，△ABC中，∠C=90°，tanA=| 4 |
| 3 |
半径为1，则阴影部分的面积S=
考点：切线的性质,扇形面积的计算
专题：
分析：连接CD，根据已知条件和切线的性质可求出AD，BC的长，进而可求△ACB的面积，利用阴影部分的面积S=S△ABC-S扇形，即可求出．
解答：解：连接CD，
∵以C为圆心的圆与AB相切于D，
∴CD⊥AB，
∵tanA=
，CD=1，
∴AD=
，
∴AC=
，
∵
=
，
∴BC=
，
∴S△ACB=
AC•BC=
，
∴S=S△ABC-S扇形=
，
故答案为：
．
∵以C为圆心的圆与AB相切于D，
∴CD⊥AB，
∵tanA=
| 4 |
| 3 |
∴AD=
| 3 |
| 4 |
∴AC=
| 5 |
| 4 |
∵
| AC |
| BC |
| 3 |
| 4 |
∴BC=
| 5 |
| 3 |
∴S△ACB=
| 1 |
| 2 |
| 25 |
| 24 |
∴S=S△ABC-S扇形=
| 25-6π |
| 24 |
故答案为：
| 25-6π |
| 24 |
点评：本题考查了圆的切线性质，及解直角三角形的知识．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．
练习册系列答案
相关题目
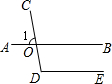已知：AB、CD相交于点O，∠1=80°，如果DE∥AB，求∠D的度数为
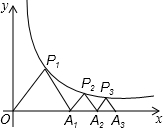如图，P1、P2、P3…Pn（n为正整数）分别是反比例函数y=
小辉身高1.65米，他在体质健康卡上填写的是165厘米，其实这是度量单位引起的数值变化：以1米为度量单位，那么他的身高就是1.65个度量单位，以1厘米为度量单位，那么他的身高就是165个度量单位．
已知：平行四边形ABCD中，过对角线AC中点O的直线EF交AD于F，BC于E．试说明BE与DF的大小关系．