题目内容
18.在一个不透明的小口布袋中装有4个标有1,2,3,4的小球,它们的质地、大小完全相同,小明从布袋里随机摸出一个小球,记下数字为x,小红在剩下的3个小球中随机摸出一个小球,记下数字为y,这样确定了点M的坐标(x,y).(1)画树状图或列表,写出点M所有可能的坐标;
(2)求点M(x,y)在函数x+y=5的图象上的概率
(3)小明和小红约定做一个游戏,其规则为:x、y若满足xy>6,则小明胜;若满足xy<6,则小红胜;这个游戏公平吗?说明理由.
分析 (1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果;
(2)由(1)可求得点M(x,y)在函数x+y=5的图象上的情况,再利用概率公式即可求得答案;
(3)首先分别求得x、y满足xy>6则小明胜,x、y满足xy<6则小红胜的概率,比较概率大小,即可得这个游戏是否公平;公平的游戏规则:只要概率相等即可.
解答 解:(1)画树状图得:
则点M所有可能的坐标有:(1,2),(1,3),(1,4),(2,1),(2,3),2,4),(3,1),(3,2),(3,4)(4,1),(4,2),(4,3)共12种;
(2)∵共有12种等可能的结果,其中在函数x+y=5的图象上的有4种:(1,4),(2,3),(3,2),(4,1),
∴点(x,y)在函数y=-x+5的图象上的概率为:$\frac{4}{12}$=$\frac{1}{3}$;
(3)这个游戏不公平.
理由:∵x、y满足xy>6有:(2,4),(3,4),(4,2),(4,3)共4种情况,
x、y满足xy<6有(1,2),(1,3),(1,4),(2,1),(3,1),(4,1)共6种情况.
∴P(小明胜)=$\frac{4}{12}$=$\frac{1}{3}$,P(小红胜)=$\frac{6}{12}$=$\frac{1}{2}$,
∴这个游戏不公平.
公平的游戏规则为:若x、y满足xy≥6则小明胜,若x、y满足xy<6则小红胜.
点评 本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.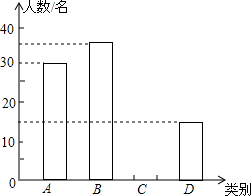 由于各地雾霾天气越来越严重,2015年春节前夕,某校团委向全校2000多名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:不会减少烟花爆竹数量;D类:使用电子鞭炮”四个选项对100名学生进行问卷调查,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:
由于各地雾霾天气越来越严重,2015年春节前夕,某校团委向全校2000多名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:不会减少烟花爆竹数量;D类:使用电子鞭炮”四个选项对100名学生进行问卷调查,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:
(1)表格中a=15,b=0.3,并补全条形统计图;
(2)如果绘制扇形统计图,请求出C类所占的圆心角的度数;
(3)根据抽样结果,请估计全校“使用电子鞭炮”的学生有多少名?
 由于各地雾霾天气越来越严重,2015年春节前夕,某校团委向全校2000多名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:不会减少烟花爆竹数量;D类:使用电子鞭炮”四个选项对100名学生进行问卷调查,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:
由于各地雾霾天气越来越严重,2015年春节前夕,某校团委向全校2000多名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:不会减少烟花爆竹数量;D类:使用电子鞭炮”四个选项对100名学生进行问卷调查,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:| 类别 | 频数 | 频率 |
| A | 30 | b |
| B | 35 | 0.35 |
| C | 20 | 0.20 |
| D | a | 0.15 |
| 合计 | 100 | 1.00 |
(2)如果绘制扇形统计图,请求出C类所占的圆心角的度数;
(3)根据抽样结果,请估计全校“使用电子鞭炮”的学生有多少名?
13. 如图所示,A为河岸上的码头,B为河中的一只小船,那么这只小船的位置确定方法不能是( )
如图所示,A为河岸上的码头,B为河中的一只小船,那么这只小船的位置确定方法不能是( )
 如图所示,A为河岸上的码头,B为河中的一只小船,那么这只小船的位置确定方法不能是( )
如图所示,A为河岸上的码头,B为河中的一只小船,那么这只小船的位置确定方法不能是( )| A. | 以A为原点,河岸为x轴,建立直角坐标系来确定 | |
| B. | 以A为原点,河岸为y轴,建立直角坐标系来确定 | |
| C. | 以AB间的距离和B在A的北偏东若干度来确定 | |
| D. | 以B为原点,平行于河岸的直线为x轴,建立直角坐标系来确定 |