题目内容
7.若△ABC内接于⊙O,∠AOB=120°,则圆周角∠ACB的度数60°或120°.分析 分点C在优弧和劣弧上两种情况,当点C在优弧上时,可直接利用圆周角定理得到∠ACB是∠AOB的一半,当点C在劣弧上时,可以优弧上找点D,则可求得∠ADB是∠AOB的一半,再利用圆内接四边形的性质可求得∠ACB
解答  解:如图1,当点C在优弧上时,
解:如图1,当点C在优弧上时,
则∠ACB=$\frac{1}{2}$∠AOB=60°;
如图2,
当点C在劣弧上时,
在优弧上找点D,
连接DA、DB,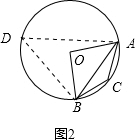 则可得∠ADB=$\frac{1}{2}$∠AOB=60°,
则可得∠ADB=$\frac{1}{2}$∠AOB=60°,
又∵四边形ACBD为圆的内接四边形,
∴∠ADB+∠ACB=180°,
∴∠ACB=180°-60°=120°,
∴∠ACB的度数是60°或120°;
故答案为:60°或120°.
点评 本题主要考查圆周角定理、圆内接四边形的性质,分点C在优弧和劣弧上两种情况进行讨论是解题的关键.

练习册系列答案
相关题目
15.-$\frac{1}{3}$的绝对值是( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
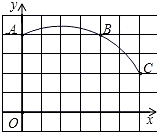 如图,直角坐标系中一条圆弧经过A(0,4),B(4,4),C(6,2)三个网格点,已知点D为x正半轴上的一点,若直线CD与该圆弧相切,则点D的坐标为(7,0).
如图,直角坐标系中一条圆弧经过A(0,4),B(4,4),C(6,2)三个网格点,已知点D为x正半轴上的一点,若直线CD与该圆弧相切,则点D的坐标为(7,0). 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到长方形OABC的边时反弹,反弹后的路径与长方形的边的夹角为45°,第1次碰到长方形边上的点的坐标为(3,0),则第17次碰到长方形边上的点的坐标为(1,4).
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到长方形OABC的边时反弹,反弹后的路径与长方形的边的夹角为45°,第1次碰到长方形边上的点的坐标为(3,0),则第17次碰到长方形边上的点的坐标为(1,4).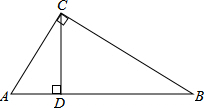 在△ABC中,∠C=90°,∠B=30°,AC=5$\sqrt{2}$,BC=5$\sqrt{6}$,CD⊥AB于点D.
在△ABC中,∠C=90°,∠B=30°,AC=5$\sqrt{2}$,BC=5$\sqrt{6}$,CD⊥AB于点D.