题目内容
3．将代数式（a-b+c-d）（a+b-c-d）写成（M+N）（M-N）的形式正确的是（ ）| A． | [a-（b+c-d）][a+（b-c-d）] | B． | [（a-b+d）+c][（a+b-d）-c] | C． | [（a-d）+（c-b）][（a-d）-（c-b）] | D． | [（a-b）+（c-d）][（a+b）-（c-d）] |
分析 直接利用添括号法则结合各项符号进而得出符合题意的答案．
解答 解：（a-b+c-d）（a+b-c-d）
=[（a-d）+（c-b）][（a-d）-（c-b）]．
故选：C．
点评 此题主要考查了添括号法则，正确添括号是解题关键．
练习册系列答案
相关题目
13．当a，b互为相反数时，代数式a2+ab-2的值为（ ）
| A． | 2 | B． | 0 | C． | -2 | D． | -1 |
11．函数y=x|x|-3x+1的图象与x轴交点的个数为（ ）
| A． | 4 | B． | 3 | C． | 2 | D． | 0 |
18．按如图的运算程序，能使输出结果为3的x，y的值是（ ）
| A． | x=5，y=-2 | B． | x=3，y=-3 | C． | x=-4，y=2 | D． | x=-3，y=-9 |
8．
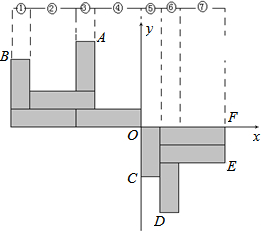用如图大小形状完全相同的长方形纸片在直角坐标系中摆成以下图案，已知A（-2，6）．
（1）求出长方形的长与宽；
（2）写出B、C、D、E、F点的坐标；
（3）要使点P（m，n）在长方形纸片拼成的图案阴影内（可以在边上），在下面的表中填写：m在哪一范围内取值时，n对应的范围是什么．
用如图大小形状完全相同的长方形纸片在直角坐标系中摆成以下图案，已知A（-2，6）．（1）求出长方形的长与宽；
（2）写出B、C、D、E、F点的坐标；
（3）要使点P（m，n）在长方形纸片拼成的图案阴影内（可以在边上），在下面的表中填写：m在哪一范围内取值时，n对应的范围是什么．
| 范围顺序号 | m的范围 | n对应的范围 |
| 1 | -2≤m≤0 | 0$≤n≤\frac{4}{3}$ |
| 2 | -$\frac{10}{3}$≤m＜-2 | 0≤n≤6 |
| 3 | -$\frac{16}{3}$≤m＜-$\frac{10}{3}$ | 0≤n≤$\frac{8}{3}$ |
| 4 | -$\frac{20}{3}$≤m＜-$\frac{16}{3}$ | 0$≤n≤\frac{14}{3}$ |
| 5 | 0＜m$≤\frac{4}{3}$ | -$\frac{10}{3}$≤n≤0 |
| 6 | $\frac{4}{3}$＜m≤$\frac{8}{3}$ | -6≤n≤0 |
| 7 | $\frac{8}{3}$＜m≤$\frac{14}{3}$ | 0≤n≤-$\frac{8}{3}$ |
12．
如图，已知△ABC与△DEF分别是等边三角形和等腰直角三角形，AC与DF交于点G，AD与FC分别是△ABC和△DEF的高，线段BC，DE在同一条直线上，则下列说法不正确的是（ ）
如图，已知△ABC与△DEF分别是等边三角形和等腰直角三角形，AC与DF交于点G，AD与FC分别是△ABC和△DEF的高，线段BC，DE在同一条直线上，则下列说法不正确的是（ ）| A． | △AGD∽△CGF | B． | △AGD∽△DGC | C． | $\frac{{S}_{△AGD}}{{S}_{△CGF}}$=3 | D． | $\frac{AG}{CG}$=$\sqrt{3}$ |