题目内容
 为促进区域经济的快速发展,加快铁路建设,洛堪铁路娄邵段复线工程经过我县甘棠镇.在甘棠镇内铁路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38,
为促进区域经济的快速发展,加快铁路建设,洛堪铁路娄邵段复线工程经过我县甘棠镇.在甘棠镇内铁路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38,| 3 |
考点:解直角三角形的应用
专题:
分析:首先过点C作CD⊥AB于D,然后在Rt△BCD中,利用三角函数的知识,求得BD,CD的长,继而在Rt△ACD中,利用∠CAB的正切求得AD的长,继而求得答案.
解答: 解:过点C作CD⊥AB于D,
解:过点C作CD⊥AB于D,
∵BC=200m,∠CBA=30°,
∴在Rt△BCD中,CD=
BC=100m,
BD=BC•cos30°=200×
=100
≈173.0(m).
∵∠CAB=54°,
∴在Rt△ACD中,AD=
=
≈
≈72.5(m).
∴AB=AD+BD≈173.0+72.5=245.5≈246(m).
答:隧道AB的长为246m.
 解:过点C作CD⊥AB于D,
解:过点C作CD⊥AB于D,∵BC=200m,∠CBA=30°,
∴在Rt△BCD中,CD=
| 1 |
| 2 |
BD=BC•cos30°=200×
| ||
| 2 |
| 3 |
∵∠CAB=54°,
∴在Rt△ACD中,AD=
| CD |
| tan∠CAB |
| CD |
| tan540 |
| 100 |
| 1.38 |
∴AB=AD+BD≈173.0+72.5=245.5≈246(m).
答:隧道AB的长为246m.
点评:此题考查了解直角三角形的应用.此题难度适中,注意掌握辅助线的作法,注意把实际问题转化为数学问题求解.

练习册系列答案
相关题目
下列方程组中,解是
的是( )
|
A、
| |||||
B、
| |||||
C、
| |||||
D、
|

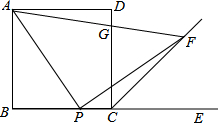 如图,在正方形ABCD中,AB=2,点P是边BC上的任意一点,E是BC延长线上一点,联结AP,作PF⊥AP交∠DCE的平分线CF上一点F,联结AF交边CD于点G.
如图,在正方形ABCD中,AB=2,点P是边BC上的任意一点,E是BC延长线上一点,联结AP,作PF⊥AP交∠DCE的平分线CF上一点F,联结AF交边CD于点G.
 如图,正方形ABCD的边长为1,以BC、CD为直径在正方形内作半圆,则阴影部分的面积是
如图,正方形ABCD的边长为1,以BC、CD为直径在正方形内作半圆,则阴影部分的面积是