Question

10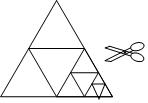．如图，将一张等边三角形纸片沿中位线剪成4个小三角形，称为第一次操作；然后，将其中的一个三角形按同样方式再剪成4个小三角形，共得到7个小三角形，称为第二次操作；再将其中一个三角形按同样方式再剪成4个小三角形，共得到10个小三角形，称为第三次操作；…根据以上操作，若要得到100个小三角形，则需要操作的次数是33．

Answer 1

分析 由第一次操作后三角形共有4个、第二次操作后三角形共有（4+3）个、第三次操作后三角形共有（4+3+3）个，可得第n次操作后三角形共有4+3（n-1）=3n+1个，根据题意得3n+1=100，求得n的值即可．

解答 解：∵第一次操作后，三角形共有4个；
第二次操作后，三角形共有4+3=7个；
第三次操作后，三角形共有4+3+3=10个；
…
∴第n次操作后，三角形共有4+3（n-1）=3n+1个；
当3n+1=100时，解得：n=33，
故答案为：33．

点评 此题主要考查了图形的变化类问题以及三角形中位线定理的运用，根据已知得出第n次操作后，三角形的个数为3n+1是解题关键．