题目内容
如图甲,二次函数y=ax2+bx+5图象的顶点为Q,与x轴交于A(-1,0)、B(5,0)两点,与y轴交于点C.

(1)求该二次函数图象顶点Q的坐标;
(2)如图乙,若点D是第一象限该函数图象上的一个动点,过D作DE⊥x轴,垂足为E.
①有一个同学说:“在第一象限函数图象上的所有点中,该函数图象的顶点Q与x轴相距最远,所以当点D运动至点Q时,折线D-E-O的长度最长”,这个同学的说法正确吗?请说明理由.
②试探究:四边形DCEB能否为平行四边形?若能,请直接写出点D的坐标;若不能,请简要说明理由.

(1)求该二次函数图象顶点Q的坐标;
(2)如图乙,若点D是第一象限该函数图象上的一个动点,过D作DE⊥x轴,垂足为E.
①有一个同学说:“在第一象限函数图象上的所有点中,该函数图象的顶点Q与x轴相距最远,所以当点D运动至点Q时,折线D-E-O的长度最长”,这个同学的说法正确吗?请说明理由.
②试探究:四边形DCEB能否为平行四边形?若能,请直接写出点D的坐标;若不能,请简要说明理由.
考点:二次函数综合题
专题:
分析:(1)将A(-1,0)、B(5,0)分别代入y=ax2+bx+5中即可确定a、b的值,然后配方后即可确定其顶点坐标;
(2)①设D(t,-t2+4t+5),设折线D-E-O的长度为L,求得L的最大值后与当点D与Q重合时L=9+2=11<
相比较即可得到答案;
②假设四边形DCEB为平行四边形,则可得到EF=DF,CF=BF.然后根据DE∥y轴求得DF,得到DF>EF,这与EF=DF相矛盾,从而否定是平行四边形.
(2)①设D(t,-t2+4t+5),设折线D-E-O的长度为L,求得L的最大值后与当点D与Q重合时L=9+2=11<
| 45 |
| 4 |
②假设四边形DCEB为平行四边形,则可得到EF=DF,CF=BF.然后根据DE∥y轴求得DF,得到DF>EF,这与EF=DF相矛盾,从而否定是平行四边形.
解答:解:(1)将A(-1,0)、B(5,0)分别代入y=ax2+bx+5中,
得
,解得
,
∴二次函数为y=-x2+4x+5.
∵y=-x2+4x+5=-(x-2)2+9,
∴Q(2,9).
(2)①这个同学的说法不正确.
∵设D(t,-t2+4t+5),设折线D-E-O的长度为L,则L=-t2+4t+5+t=-t2+5t+5=-(t-
)2+
,
∵a<0,
∴当t=
时,L最大值=
.
而当点D与Q重合时,L=9+2=11<
,
∴该该同学的说法不正确.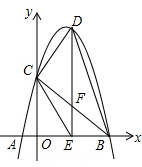
②四边形DCEB不能为平行四边形.
如图,若四边形DCEB为平行四边形,则EF=DF,CF=BF.
∵DE∥y轴,
∴
=
=1,即OE=BE=2.5.
当xF=2.5时,yF=-2.5+5=2.5,即EF=2.5;
当xD=2.5时,yD=-(2.5-2)2+9=8.75,即DE=8.75.
∴DF=DE-EF=8.75-2.5=6.25>2.5.即DF>EF,这与EF=DF相矛盾,
∴四边形DCEB不能为平行四边形.
得
|
|
∴二次函数为y=-x2+4x+5.
∵y=-x2+4x+5=-(x-2)2+9,
∴Q(2,9).
(2)①这个同学的说法不正确.
∵设D(t,-t2+4t+5),设折线D-E-O的长度为L,则L=-t2+4t+5+t=-t2+5t+5=-(t-
| 5 |
| 2 |
| 45 |
| 4 |
∵a<0,
∴当t=
| 5 |
| 2 |
| 45 |
| 4 |
而当点D与Q重合时,L=9+2=11<
| 45 |
| 4 |
∴该该同学的说法不正确.

②四边形DCEB不能为平行四边形.
如图,若四边形DCEB为平行四边形,则EF=DF,CF=BF.
∵DE∥y轴,
∴
| OE |
| EB |
| CF |
| BF |
当xF=2.5时,yF=-2.5+5=2.5,即EF=2.5;
当xD=2.5时,yD=-(2.5-2)2+9=8.75,即DE=8.75.
∴DF=DE-EF=8.75-2.5=6.25>2.5.即DF>EF,这与EF=DF相矛盾,
∴四边形DCEB不能为平行四边形.
点评:本题考查了二次函数的综合知识,其中涉及到的知识点有抛物线的顶点的确定方法及有关的几何知识.在求有关动点问题时要注意分析题意分情况讨论结果.

练习册系列答案
相关题目
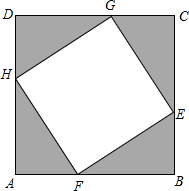 一张正方形纸板的边长为10cm,将它割去一个正方形,留下四个全等的直角三角形(图中阴影部分面积),设AH=BF=CG=DH=x(cm).阴影部分的面积为y(cm2),求,
一张正方形纸板的边长为10cm,将它割去一个正方形,留下四个全等的直角三角形(图中阴影部分面积),设AH=BF=CG=DH=x(cm).阴影部分的面积为y(cm2),求,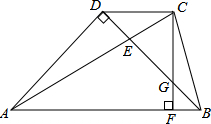 如图,梯形ABCD中,CD∥AB,△ABD为等腰直角三角形,AC=AB,AC与BD相交于E点,CF⊥AB于点F,交BD于G点,下列结论:(1)BE=BC;(2)BC=
如图,梯形ABCD中,CD∥AB,△ABD为等腰直角三角形,AC=AB,AC与BD相交于E点,CF⊥AB于点F,交BD于G点,下列结论:(1)BE=BC;(2)BC=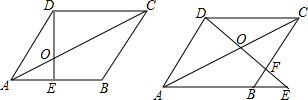
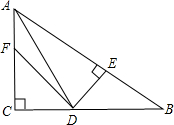 如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF; 已知:如图,AB∥CD,∠B=33°,∠E=12°,则∠D的度数为
已知:如图,AB∥CD,∠B=33°,∠E=12°,则∠D的度数为