题目内容
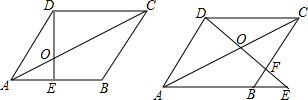
如图,在平行四边形ABCD中,O是对角线AC上一动点,连接DO并延长交AB于点E,得到的△DOC与△EOA相似.
(1)当O点运动到何处时,△DOC与△EOA的相似比为2?
(2)当O点运动到何处时,△DOC与△EOA全等?
(3)当O点运动到何处时E与B重合?此时△DOC与△EOA的相似比是多少?此时O点继续往C点运动,DO的延长线于BC交于F,且有△DFC∽△EFB,当点F是BC中点时,求△DOC与△EOA的相似比.

(1)当O点运动到何处时,△DOC与△EOA的相似比为2?
(2)当O点运动到何处时,△DOC与△EOA全等?
(3)当O点运动到何处时E与B重合?此时△DOC与△EOA的相似比是多少?此时O点继续往C点运动,DO的延长线于BC交于F,且有△DFC∽△EFB,当点F是BC中点时,求△DOC与△EOA的相似比.
考点:相似形综合题
专题:
分析:(1)根据若△DOC与△EOA的相似比为2,则
=2,即可得出当O点运动到
=2处时,△DOC与△EOA的相似比为2,
(2)若△DOC与△EOA全等,则AO=CO,根据∠CDO=∠AEO,∠DCO=∠EAO,证出△DOC≌△EOA,即可得出当O点运动到AC的中点处时,△DOC与△EOA全等;
(3)当E与B重合时,△DOC与△EOA全等,AO=CO,当O点运动到AC的中点处时,E与B重合,此时△DOC与△EOA的相似比是1,当点F是BC中点时,则BF=CF,再根据∠CDF=∠BEF,∠DCF=∠EBF,证出△DOC≌△EOA从而得出AB=DC=BE,最后求出
=
,即可得出△DOC与△EOA的相似比.
| CO |
| AO |
| CO |
| AO |
(2)若△DOC与△EOA全等,则AO=CO,根据∠CDO=∠AEO,∠DCO=∠EAO,证出△DOC≌△EOA,即可得出当O点运动到AC的中点处时,△DOC与△EOA全等;
(3)当E与B重合时,△DOC与△EOA全等,AO=CO,当O点运动到AC的中点处时,E与B重合,此时△DOC与△EOA的相似比是1,当点F是BC中点时,则BF=CF,再根据∠CDF=∠BEF,∠DCF=∠EBF,证出△DOC≌△EOA从而得出AB=DC=BE,最后求出
| DC |
| AE |
| 1 |
| 2 |
解答:解:(1)∵若△DOC与△EOA的相似比为2,则
=2,
∴当O点运动到
=2处时,△DOC与△EOA的相似比为2;
(2)若△DOC与△EOA全等,则AO=CO,
∵AB∥CD,
∴∠CDO=∠AEO,∠DCO=∠EAO,
在△DOC与△EOA中,
∴△DOC≌△EOA,
∴当O点运动到AC的中点处时,△DOC与△EOA全等;
(3)∵当E与B重合时,△DOC与△EOA全等,
∴AO=CO,
∴当O点运动到AC的中点处时,E与B重合,
此时△DOC与△EOA的相似比是1,
当点F是BC中点时,则BF=CF,
∵AB∥CD,
∴∠CDF=∠BEF,∠DCF=∠EBF,
在△DOC和△EOA中
,
∴△DOC≌△EOA,
∴DC=BE,
∴AB=DC=BE,
∴
=
,
∴△DOC与△EOA的相似比=
=
.
| CO |
| AO |
∴当O点运动到
| CO |
| AO |
(2)若△DOC与△EOA全等,则AO=CO,
∵AB∥CD,
∴∠CDO=∠AEO,∠DCO=∠EAO,
在△DOC与△EOA中,
|
∴△DOC≌△EOA,
∴当O点运动到AC的中点处时,△DOC与△EOA全等;
(3)∵当E与B重合时,△DOC与△EOA全等,
∴AO=CO,
∴当O点运动到AC的中点处时,E与B重合,
此时△DOC与△EOA的相似比是1,
当点F是BC中点时,则BF=CF,
∵AB∥CD,
∴∠CDF=∠BEF,∠DCF=∠EBF,

在△DOC和△EOA中
|
∴△DOC≌△EOA,
∴DC=BE,
∴AB=DC=BE,
∴
| DC |
| AE |
| 1 |
| 2 |
∴△DOC与△EOA的相似比=
| DC |
| AE |
| 1 |
| 2 |
点评:此题考查了相似形综合,用到的知识点是相似三角形和全等三角形的判定与性质、平行四边形的性质,关键是综合运用有关性质求出对应线段的比.

练习册系列答案
相关题目
 如图所示,AB与BC被AD所截得的内错角是
如图所示,AB与BC被AD所截得的内错角是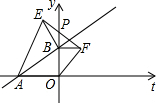 如图,平面直角坐标系中点A的坐标为(-4,0),点B的坐标为(0,m)(其中m>0).
如图,平面直角坐标系中点A的坐标为(-4,0),点B的坐标为(0,m)(其中m>0).
 (用反证法证明)已知直线a∥c,b∥c,求证:a∥b.
(用反证法证明)已知直线a∥c,b∥c,求证:a∥b.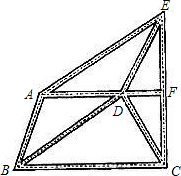 某市增强“公车”监视机制,提倡办公职员以步代车.如图所示,是该市部门街道表示图,A、D、F在同一直线上,BA∥DE,BD∥AE,F是CE的中点,求证:DE=CD.
某市增强“公车”监视机制,提倡办公职员以步代车.如图所示,是该市部门街道表示图,A、D、F在同一直线上,BA∥DE,BD∥AE,F是CE的中点,求证:DE=CD.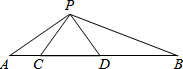 如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB.
如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB.