题目内容
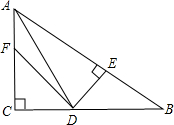 如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;(1)求证:CF=EB;
(2)若AC=8,CD=4,求四边形AFDB的面积.
考点:全等三角形的判定与性质,角平分线的性质
专题:
分析:(1)根据角平分线的性质,可得DE与CD的关系,根据HL,可得△BDE与△FDC间的关系,根据全等三角形的性质,可得答案;
(2)根据相似三角形的判定与性质,可得EB的长,根据根据勾股定理,可得FD的长,再根据面积的和差,可得答案.
(2)根据相似三角形的判定与性质,可得EB的长,根据根据勾股定理,可得FD的长,再根据面积的和差,可得答案.
解答:(1)证明:∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,
∴CD=DE.
在Rt△CDF和Rt△EDB中,
,
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB;
(2)设BE的长是x,
∵∠B=∠B,∠BED=∠BCA,
∴△BED∽△BCA,
∴
=
=
,
解得x=
,CF=EB=
BC=4+
=
+4=
,
S四边形AFDB=S△ABC-S△CFD
=
AC•BC-
CF•CD
=
×8×
-
×
×4
=32
∴CD=DE.
在Rt△CDF和Rt△EDB中,
|
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB;
(2)设BE的长是x,
∵∠B=∠B,∠BED=∠BCA,
∴△BED∽△BCA,
∴
| BE |
| BC |
| DE |
| AC |
| x | ||
4+
|
| 4 |
| 8 |
解得x=
| 16 |
| 3 |
| 16 |
| 3 |
BC=4+
(
|
|
| 32 |
| 3 |
S四边形AFDB=S△ABC-S△CFD
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 32 |
| 3 |
| 1 |
| 2 |
| 16 |
| 3 |
=32
点评:本题考查了全等三角形的判定与性质,利用了全等三角形的判定与性质,相似三角形的判定与性质,面积的和差.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
在-0.5,0,0.5,1这四个数中,最小的数是( )
| A、-0.5 | B、0.5 | C、0 | D、1 |

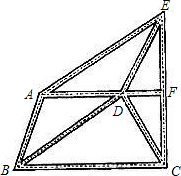 某市增强“公车”监视机制,提倡办公职员以步代车.如图所示,是该市部门街道表示图,A、D、F在同一直线上,BA∥DE,BD∥AE,F是CE的中点,求证:DE=CD.
某市增强“公车”监视机制,提倡办公职员以步代车.如图所示,是该市部门街道表示图,A、D、F在同一直线上,BA∥DE,BD∥AE,F是CE的中点,求证:DE=CD.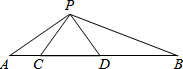 如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB.
如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB.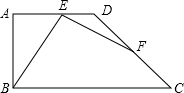 如图,梯形ABCD,AD∥BC,∠ABC=2∠BCD=90°,点E在AD上,点F在DC上,∠BEF=∠A,AB=AD,试猜想EB和EF的数量关系.
如图,梯形ABCD,AD∥BC,∠ABC=2∠BCD=90°,点E在AD上,点F在DC上,∠BEF=∠A,AB=AD,试猜想EB和EF的数量关系.