题目内容
百货公司发现某品牌服装每天可出售20件,每件赢利40元,为扩大销量增盈利,减少库存,商场决定采取适当的降价措施,经市场调查发现:每件衣服每降价4元,平均每天可多售出8件.
(1)若要想平均每天销售服装盈利1200元,那么每件应降价多少元?
(2)要使该商场销售这种服装平均每天获得的利润最大,则这种服装应如何定价?
(1)若要想平均每天销售服装盈利1200元,那么每件应降价多少元?
(2)要使该商场销售这种服装平均每天获得的利润最大,则这种服装应如何定价?
考点:二次函数的应用,一元二次方程的应用
专题:
分析:(1)可设每件服装应降价x元,则每件赢利(40-x)元,平均每天可售出(20+2x)件,根据每件的盈利×销售的件数=服装的盈利,据此即可列出方程,求出答案;
(2)根据函数关系式,运用函数的性质求最值.
(2)根据函数关系式,运用函数的性质求最值.
解答:解:(1)设每件服装应降价x元,则
(40-x)(20+2x)=1200,
解得:x=10或20,
又∵扩大销量,
∴取x=20.
答:每件这种商品应降价20元.
(2)商场每天盈利(40-x)(20+2x)=-2(x-15)2+1250,
当x=15元时,商场盈利最多,共1250元.
答:每件服装降价15元时,商场平均每天盈利最多.
(40-x)(20+2x)=1200,
解得:x=10或20,
又∵扩大销量,
∴取x=20.
答:每件这种商品应降价20元.
(2)商场每天盈利(40-x)(20+2x)=-2(x-15)2+1250,
当x=15元时,商场盈利最多,共1250元.
答:每件服装降价15元时,商场平均每天盈利最多.
点评:此题考查了一元二次方程的应用以及二次函数的应用,此题首先要正确理解题意,把实际问题的数量关系转化为一元二次方程求解,但应注意考虑解应符合的条件,即考虑解的取舍.

练习册系列答案
相关题目
在-0.5,0,0.5,1这四个数中,最小的数是( )
| A、-0.5 | B、0.5 | C、0 | D、1 |
 如图所示,AB与BC被AD所截得的内错角是
如图所示,AB与BC被AD所截得的内错角是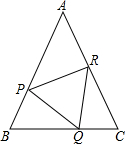 如图,在△ABC中,AB=AC,P、Q、R分别在AB、AC上,且BP=CQ,BQ=CR.
如图,在△ABC中,AB=AC,P、Q、R分别在AB、AC上,且BP=CQ,BQ=CR.
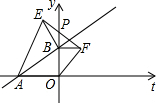 如图,平面直角坐标系中点A的坐标为(-4,0),点B的坐标为(0,m)(其中m>0).
如图,平面直角坐标系中点A的坐标为(-4,0),点B的坐标为(0,m)(其中m>0).
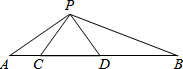 如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB.
如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB.