题目内容
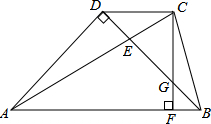 如图,梯形ABCD中,CD∥AB,△ABD为等腰直角三角形,AC=AB,AC与BD相交于E点,CF⊥AB于点F,交BD于G点,下列结论:(1)BE=BC;(2)BC=
如图,梯形ABCD中,CD∥AB,△ABD为等腰直角三角形,AC=AB,AC与BD相交于E点,CF⊥AB于点F,交BD于G点,下列结论:(1)BE=BC;(2)BC=| 2 |
考点:全等三角形的判定与性质,等腰三角形的性质,梯形
专题:
分析:过点D作DH⊥AB于H,得到四边形CDHF是矩形,根据矩形的对边相等可得CF=DH,根据等腰直角三角形的性质可得DH=
AB,然后根据直角三角形30°角所对的直角边等于斜边的一半求出∠BAC=30°,再求出∠BCE=∠BEC=75°,根据等角对等边可得BE=BC,判断出(1)正确;过点C作CK⊥BD于K,判断出△CDK为等腰直角三角形,根据等腰直角三角形的性质可得CK=
CD,再根据直角三角形30°角所对的直角边等于斜边的一半求出BC=CK,然后整理判断出(2)正确;过点B作BM⊥CE于M,根据等腰三角形三线合一的性质可得CE=2CM,再求出∠CBM=∠BCF=15°,利用“角角边”证明△BCM和△CBF全等,根据全等三角形对应边相等可得BF=CM,然后判断出(3)正确.
| 1 |
| 2 |
| ||
| 2 |
解答: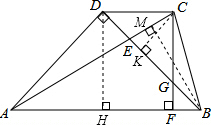 解:如图,过点D作DH⊥AB于H,∵CD∥AB,CF⊥AB,
解:如图,过点D作DH⊥AB于H,∵CD∥AB,CF⊥AB,
∴四边形CDHF是矩形,
∴CF=DH,
∵△ABD为等腰直角三角形,
∴DH=
AB,
∵AB=AC,
∴CF=
AC,
∴∠BAC=30°,
∴∠BCE=
(180°-30°)=75°,
∵∠BEC=∠BAC+∠ABD=30°+45°=75°,
∴∠BCE=∠BEC=75°,
∴BE=BC,故(1)正确;
过点C作CK⊥BD于K,
∵CD∥AB,
∴∠CDK=∠ABD=45°,
∴△CDK为等腰直角三角形,
∴CK=
CD,
∵∠CBD=∠ABC-∠ABD=75°-45°=30°,
∴BC=2CK,
∴BC=2×
CD=
CD,故(2)正确;
过点B作BM⊥CE于M,
∵BC=BE,∠CBD=30°,
∴CE=2CM,∠CBM=15°,
∵∠BCF=90°-∠ABC=90°-75°=15°,
∴∠CBM=∠BCF=15°,
在△BCM和△CBF中,
,
∴△BCM≌△CBF(AAS),
∴BF=CM,
∴CE=2BF,故(3)正确.
综上所述,正确的是(1)(2)(3).
 解:如图,过点D作DH⊥AB于H,∵CD∥AB,CF⊥AB,
解:如图,过点D作DH⊥AB于H,∵CD∥AB,CF⊥AB,∴四边形CDHF是矩形,
∴CF=DH,
∵△ABD为等腰直角三角形,
∴DH=
| 1 |
| 2 |
∵AB=AC,
∴CF=
| 1 |
| 2 |
∴∠BAC=30°,
∴∠BCE=
| 1 |
| 2 |
∵∠BEC=∠BAC+∠ABD=30°+45°=75°,
∴∠BCE=∠BEC=75°,
∴BE=BC,故(1)正确;
过点C作CK⊥BD于K,
∵CD∥AB,
∴∠CDK=∠ABD=45°,
∴△CDK为等腰直角三角形,
∴CK=
| ||
| 2 |
∵∠CBD=∠ABC-∠ABD=75°-45°=30°,
∴BC=2CK,
∴BC=2×
| ||
| 2 |
| 2 |
过点B作BM⊥CE于M,
∵BC=BE,∠CBD=30°,
∴CE=2CM,∠CBM=15°,
∵∠BCF=90°-∠ABC=90°-75°=15°,
∴∠CBM=∠BCF=15°,
在△BCM和△CBF中,
|
∴△BCM≌△CBF(AAS),
∴BF=CM,
∴CE=2BF,故(3)正确.
综上所述,正确的是(1)(2)(3).
点评:本题考查了全等三角形的判定与性质,等腰三角形的判定与性质,等腰直角三角形的性质,直角梯形,难点在于作辅助线,构造出矩形,等腰三角形和全等三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

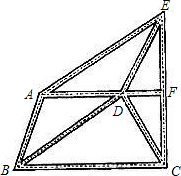 某市增强“公车”监视机制,提倡办公职员以步代车.如图所示,是该市部门街道表示图,A、D、F在同一直线上,BA∥DE,BD∥AE,F是CE的中点,求证:DE=CD.
某市增强“公车”监视机制,提倡办公职员以步代车.如图所示,是该市部门街道表示图,A、D、F在同一直线上,BA∥DE,BD∥AE,F是CE的中点,求证:DE=CD.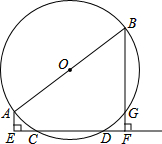 如图,AB是⊙O的直径,CD是弦,AE⊥CD于E,BF⊥CD于F,BF交⊙O于G,下面的结论:(1)EC=DF;(2)AE+BF=AB;(3)AE=GF;(4)FG•FB=EC•ED;其中正确的结论是
如图,AB是⊙O的直径,CD是弦,AE⊥CD于E,BF⊥CD于F,BF交⊙O于G,下面的结论:(1)EC=DF;(2)AE+BF=AB;(3)AE=GF;(4)FG•FB=EC•ED;其中正确的结论是