题目内容
6.设$\vec e$是单位向量,$\vec a$是非零向量,则下列式子中正确的是( )| A. | $|{\vec a}|$$\vec e$=$\vec a$ | B. | $\vec a$$|{\vec e}|$=$\vec a$ | C. | $\frac{1}{\vec a}$$\vec a$=$\vec e$ | D. | $\frac{{|{\vec a}|}}{{|{\vec e}|}}$=$\vec a$ |
分析 单位向量是指模等于1的向量.由于是非零向量,单位向量具有确定的方向.
一个非零向量除以它的模,可得与其方向相同的单位向量.
单位向量有无数个;不同的单位向量,是指它们的方向不同.
解答 解:A、∵单位向量$\vec e$与非零向量$\vec a$的方向不一定相同,
∴|$\overrightarrow{a}$|$\overrightarrow{e}$=$\overrightarrow{a}$不一定成立,故本选项错误;
B、$\overrightarrow{a}$|$\overrightarrow{e}$|=$\overrightarrow{a}$,原式计算正确;故本选项正确;
C、$\frac{1}{\overrightarrow{a}}\overrightarrow{a}$=1,原式计算错误;故本选项错误;
D、$\frac{|\overrightarrow{a|}}{|\overrightarrow{e}|}$=|$\overrightarrow{a}$|,原式计算错误;故本选项错误.
故选:B.
点评 本题主要考查了平面向量的模与向量的一些基础知识,应熟练掌握一个非零向量除以它的模,可得与其方向相同的单位向量.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
16.式子x2y,$-\frac{8}{7}mn$,$\frac{1}{2}$,3s-1,0,m,$\frac{a+b}{5}$,$\frac{y}{x}$中单项式有( )
| A. | 4个 | B. | 6个 | C. | 5个 | D. | 7个 |
15.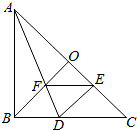 如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE、EF,下列结论:①AB=2BD;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点O不一定落在AC上;④BD=BF,上述结论中正确的是( )
如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE、EF,下列结论:①AB=2BD;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点O不一定落在AC上;④BD=BF,上述结论中正确的是( )
 如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE、EF,下列结论:①AB=2BD;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点O不一定落在AC上;④BD=BF,上述结论中正确的是( )
如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE、EF,下列结论:①AB=2BD;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点O不一定落在AC上;④BD=BF,上述结论中正确的是( )| A. | ①②③④ | B. | ②④ | C. | ①③④ | D. | ①②④ |
16.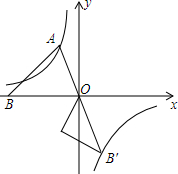 如图,已知第二象限的点A在反比例函数y=-$\frac{\sqrt{3}}{x}$上,过点A作AB⊥AO交x轴于点B,∠AOB=60°.将△AOB绕点O逆时针旋转120°,点B的对应点B′恰好落在反比例函数y=$\frac{k}{x}$上,则k的值为( )
如图,已知第二象限的点A在反比例函数y=-$\frac{\sqrt{3}}{x}$上,过点A作AB⊥AO交x轴于点B,∠AOB=60°.将△AOB绕点O逆时针旋转120°,点B的对应点B′恰好落在反比例函数y=$\frac{k}{x}$上,则k的值为( )
 如图,已知第二象限的点A在反比例函数y=-$\frac{\sqrt{3}}{x}$上,过点A作AB⊥AO交x轴于点B,∠AOB=60°.将△AOB绕点O逆时针旋转120°,点B的对应点B′恰好落在反比例函数y=$\frac{k}{x}$上,则k的值为( )
如图,已知第二象限的点A在反比例函数y=-$\frac{\sqrt{3}}{x}$上,过点A作AB⊥AO交x轴于点B,∠AOB=60°.将△AOB绕点O逆时针旋转120°,点B的对应点B′恰好落在反比例函数y=$\frac{k}{x}$上,则k的值为( )| A. | -2$\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | -4$\sqrt{3}$ |
 如图,已知AB是⊙O的弦,∠B=30°,C是弦AB上的任意一点(不与点A、B重合),连接CO并延长交⊙O于点D,连接AD.
如图,已知AB是⊙O的弦,∠B=30°,C是弦AB上的任意一点(不与点A、B重合),连接CO并延长交⊙O于点D,连接AD.