题目内容
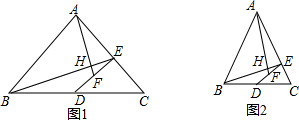
14. 如图,已知AB是⊙O的弦,∠B=30°,C是弦AB上的任意一点(不与点A、B重合),连接CO并延长交⊙O于点D,连接AD.
如图,已知AB是⊙O的弦,∠B=30°,C是弦AB上的任意一点(不与点A、B重合),连接CO并延长交⊙O于点D,连接AD.(1)当∠D=20°,求∠BOD的度数;
(2)若以A、C、D为顶点的三角形与以B、C、O为顶点的三角形相似,求∠D的度数.
分析 (1)连接OA,根据圆的半径相等证明∠OAB=∠B和∠OAD=∠D,得到答案;
(2)若以A、C、D为顶点的三角形与以B、C、O为顶点的三角形相似,由外角的性质得到∠BCO=∠CAD+∠D,推出∠ACD=∠BCO,由平角的定义得到∠ACD+∠BCO=180°,求得∠ACD=∠BCO=90°,即可得到答案.
解答 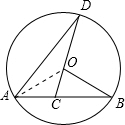 解:(1)连接OA,
解:(1)连接OA,
∵OA=OB,
∴∠OAB=∠B=30°,
∵OA=OD,
∴∠OAD=∠D=20°,
∴∠BAD=∠OAB=∠OAD=50°,
∴∠BOD=2∠BAD=100°;
(2)若以A、C、D为顶点的三角形与以B、C、O为顶点的三角形相似,
∵∠BCO=∠CAD+∠D,
∴∠ACD=∠BCO,
∵∠ACD+∠BCO=180°,
∴∠ACD=∠BCO=90°,
∴∠D=∠B=30°,或∠A=∠B=30°,
∴∠D=60°,
综上所述:以A、C、D为顶点的三角形与以B、C、O为顶点的三角形相似,∠D=30°或60°.
点评 此题考查了垂径定理,圆周角的性质以及相似三角形的性质,掌握圆的半径相等和等边对等角是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
2. 如图,在扇形OAB中,半径OA=4,∠AOB=120°,点C在$\widehat{AB}$上,OD⊥AC于点D,OE⊥BC于点E,当点C从点A运动到点B时,线段DE长度的变化情况是( )
如图,在扇形OAB中,半径OA=4,∠AOB=120°,点C在$\widehat{AB}$上,OD⊥AC于点D,OE⊥BC于点E,当点C从点A运动到点B时,线段DE长度的变化情况是( )
 如图,在扇形OAB中,半径OA=4,∠AOB=120°,点C在$\widehat{AB}$上,OD⊥AC于点D,OE⊥BC于点E,当点C从点A运动到点B时,线段DE长度的变化情况是( )
如图,在扇形OAB中,半径OA=4,∠AOB=120°,点C在$\widehat{AB}$上,OD⊥AC于点D,OE⊥BC于点E,当点C从点A运动到点B时,线段DE长度的变化情况是( )| A. | 先变小,后变大 | B. | 先变大,后变小 | ||
| C. | DE与OD的长度保持相等 | D. | 固定不变 |
6.设$\vec e$是单位向量,$\vec a$是非零向量,则下列式子中正确的是( )
| A. | $|{\vec a}|$$\vec e$=$\vec a$ | B. | $\vec a$$|{\vec e}|$=$\vec a$ | C. | $\frac{1}{\vec a}$$\vec a$=$\vec e$ | D. | $\frac{{|{\vec a}|}}{{|{\vec e}|}}$=$\vec a$ |
 如图,函数y=2x和y=ax+4的图象相交于点A(m,3)
如图,函数y=2x和y=ax+4的图象相交于点A(m,3) 如图,在菱形ABCD中,对角线BD=4$\sqrt{3}$,∠ABC=60°,对角线AC、BD交于点O,以点B为圆心,BC为半径作圆与BD交于点E,则图中阴影部分的面积为$\frac{4π}{3}$-2$\sqrt{3}$.
如图,在菱形ABCD中,对角线BD=4$\sqrt{3}$,∠ABC=60°,对角线AC、BD交于点O,以点B为圆心,BC为半径作圆与BD交于点E,则图中阴影部分的面积为$\frac{4π}{3}$-2$\sqrt{3}$.