题目内容
11．如表，给出了一个二次函数的一些取值情况：| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 3 | 0 | -1 | 0 | 3 | … |
（2）根据图象写出：当0≤y＜3时x的取值范围．
分析 （1）通过描点、连线得到抛物线；
（2）根据图象即可求得．
解答 解：（1）画图如图所示，
（2）当0≤y＜3时x的取值范围：0＜x≤1或3≤x＜4．
点评 本题主要考查对用待定系数法求二次函数的解析式，二次函数图象上点的坐标特征，二次函数的图象，抛物线与X轴的交点，能综合运用这些性质进行计算是解此题的关键．
练习册系列答案
相关题目
2．
如图，在扇形OAB中，半径OA=4，∠AOB=120°，点C在$\widehat{AB}$上，OD⊥AC于点D，OE⊥BC于点E，当点C从点A运动到点B时，线段DE长度的变化情况是（ ）
如图，在扇形OAB中，半径OA=4，∠AOB=120°，点C在$\widehat{AB}$上，OD⊥AC于点D，OE⊥BC于点E，当点C从点A运动到点B时，线段DE长度的变化情况是（ ）| A． | 先变小，后变大 | B． | 先变大，后变小 | ||
| C． | DE与OD的长度保持相等 | D． | 固定不变 |
6．设$\vec e$是单位向量，$\vec a$是非零向量，则下列式子中正确的是（ ）
| A． | $|{\vec a}|$$\vec e$=$\vec a$ | B． | $\vec a$$|{\vec e}|$=$\vec a$ | C． | $\frac{1}{\vec a}$$\vec a$=$\vec e$ | D． | $\frac{{|{\vec a}|}}{{|{\vec e}|}}$=$\vec a$ |
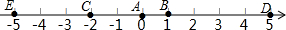如图，A点的初始位置位于数轴上的原点，现对A点做如下移动：第1次从原点向右移动1个单位长度至B点，第2次从B点向左移动3个单位长度至C点，第3次从C点向右移动6个单位长度至D点，第4次从D点向左移动9个单位长度至E点，…，依此类推，这样至少移动1001次后该点到原点的距离不小于1499．
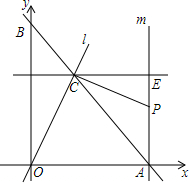如图，直线y=-x+$\sqrt{2}$分别交x轴、y轴于A、B两点，经过点A的直线m⊥x轴，直线l经过原点O交线段AB于点C，过点C作OC的垂线，与直线m相交于点P，现将直线l绕O点旋转，使交点C在线段AB上由点B向点A方向运动．