题目内容
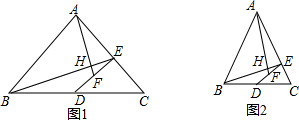
15. 如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE、EF,下列结论:①AB=2BD;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点O不一定落在AC上;④BD=BF,上述结论中正确的是( )
如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE、EF,下列结论:①AB=2BD;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点O不一定落在AC上;④BD=BF,上述结论中正确的是( )| A. | ①②③④ | B. | ②④ | C. | ①③④ | D. | ①②④ |
分析 根据折叠的知识,锐角正切值的定义,全等三角形的判定,面积的计算判断所给选项是否正确即可.
解答 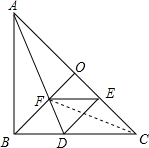 解:①由折叠可得BD=DE,∠AED=∠ABD=90°,即∠DEC=90°,
解:①由折叠可得BD=DE,∠AED=∠ABD=90°,即∠DEC=90°,
∵DC>DE,
∴DC>BD,
∴tan∠ADB≠2,故①错误;
②由翻折的性质可知:图中的全等三角形有△ABF≌△AEF,△ABD≌△AED,△FBD≌△FED.
∵OB⊥AC,
∴∠AOB=∠COB=90°,
在Rt△AOB和Rt△COB中,
$\left\{\begin{array}{l}{AB=BC}\\{BO=BO}\end{array}\right.$,
∴Rt△AOB≌Rt△COB(HL).
则全等三角形共有4对,故②正确;
③∵AB=CB,BO⊥AC,把△ABC折叠,
∴∠ABO=∠CBO=45°,∠FBD=∠DEF.
∴∠AEF=∠DEF=45°,
∴将△DEF沿EF折叠,可得点D一定在AC上,故③错误;
④∵OB⊥AC,且AB=CB,
∴BO为∠ABC的平分线,即∠ABO=∠OBC=45°.
由折叠可知,AD是∠BAC的平分线,即∠BAF=22.5°.
又∵∠BFD为三角形ABF的外角,
∴∠BFD=∠ABO+∠BAF=67.5°.
∴∠BDF=180°-45°-67.5°=67.5°.
∴∠BFD=∠BDF.
∴BD=BF,故④正确.
故选B.
点评 本题主要考查的是翻折的性质、等腰三角形的性质、全等三角形的判定、三角形外角的性质,掌握翻折的性质是解题的关键.

练习册系列答案
相关题目
6.设$\vec e$是单位向量,$\vec a$是非零向量,则下列式子中正确的是( )
| A. | $|{\vec a}|$$\vec e$=$\vec a$ | B. | $\vec a$$|{\vec e}|$=$\vec a$ | C. | $\frac{1}{\vec a}$$\vec a$=$\vec e$ | D. | $\frac{{|{\vec a}|}}{{|{\vec e}|}}$=$\vec a$ |
 如图,函数y=2x和y=ax+4的图象相交于点A(m,3)
如图,函数y=2x和y=ax+4的图象相交于点A(m,3)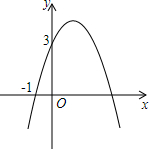 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).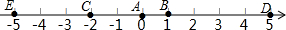 如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动1001次后该点到原点的距离不小于1499.
如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动1001次后该点到原点的距离不小于1499.