题目内容
16.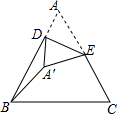 如图,△ABC中,AB=BC=AC=10,D是AB边上的动点,E是AC边的中点,将△ADE沿DE翻折得到△A′DE,连接BA′,则BA′的最小值是5$\sqrt{3}$-5.
如图,△ABC中,AB=BC=AC=10,D是AB边上的动点,E是AC边的中点,将△ADE沿DE翻折得到△A′DE,连接BA′,则BA′的最小值是5$\sqrt{3}$-5.
分析 连接BE,由等边三角形三线合一的性质可知BE⊥AC,在△BCE中,由勾股定理可求得EC的长,然后由翻折的性质可知A′E=5,由三角形的三边关系可知当点B、A′,E在一条直线上时,BA′有最小值,最小值=BE-A′E.
解答 解:如图所示:连接BE.
∵AB=BC=AC=10,
∴∠C=60°.
∵AB=BC,E是AC的中点,
∴BE⊥AC.
∴BE=$\sqrt{B{C}^{2}-E{C}^{2}}$=$\sqrt{1{0}^{2}-{5}^{2}}$=5$\sqrt{3}$.
∵AC=10,E是AC边的中点,
∴AE=5.
由翻折的性质可知A′E=AE=5.
∵BA′+A′E≥BE,
∴当点B、A′,E在一条直线上时,BA′有最小值,最小值=BE-A′E=5$\sqrt{3}$-5.
故答案为:5$\sqrt{3}$-5.
点评 本题主要考查的是翻折的性质、勾股定理的应用,明确当点B、A′,E在一条直线上时,BA′有最小值是解题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
6. 如图,Rt△ABC中,∠B=90°,AB=6,BC=9,将△ABC折叠,使C点与AB的中点D重合,折痕为EF,则线段BF的长为( )
如图,Rt△ABC中,∠B=90°,AB=6,BC=9,将△ABC折叠,使C点与AB的中点D重合,折痕为EF,则线段BF的长为( )
 如图,Rt△ABC中,∠B=90°,AB=6,BC=9,将△ABC折叠,使C点与AB的中点D重合,折痕为EF,则线段BF的长为( )
如图,Rt△ABC中,∠B=90°,AB=6,BC=9,将△ABC折叠,使C点与AB的中点D重合,折痕为EF,则线段BF的长为( )| A. | $\frac{5}{2}$ | B. | $\frac{9}{2}$ | C. | 4 | D. | 5 |
7.已知△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是70cm和48cm,则△ABC的腰和底边长分别为( )
| A. | 24cm和22cm | B. | 26cm和18cm | C. | 22cm和26cm | D. | 23cm和24cm |
4.下列运算正确的是( )
| A. | $\sqrt{5}-\sqrt{3}=\sqrt{2}$ | B. | $\sqrt{4\frac{1}{9}}=2\frac{1}{3}$ | C. | $\sqrt{8}-\sqrt{2}=\sqrt{2}$ | D. | $\sqrt{8}÷\sqrt{2}=4$ |
5. 如图所示,下列条件中,不能得到l1∥l2的是( )
如图所示,下列条件中,不能得到l1∥l2的是( )
 如图所示,下列条件中,不能得到l1∥l2的是( )
如图所示,下列条件中,不能得到l1∥l2的是( )| A. | ∠4=∠5 | B. | ∠1=∠3 | C. | ∠2=∠3 | D. | ∠2+∠4=180° |
 如图,△ABC是△DEF向右平移4个单位长度后得到的,且三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
如图,△ABC是△DEF向右平移4个单位长度后得到的,且三个顶点的坐标分别为A(1,1),B(4,2),C(3,4). 如图,CD⊥AB,垂足为D,如果CD=12,AD=16,BD=9,那么△ABC是直角三角形吗?请说明理由.
如图,CD⊥AB,垂足为D,如果CD=12,AD=16,BD=9,那么△ABC是直角三角形吗?请说明理由.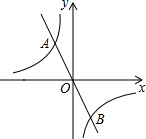 如图示,双曲线y=$\frac{{k}_{1}}{x}$与直线y=k2x交于A(-1,m)、B(n,-2)两点
如图示,双曲线y=$\frac{{k}_{1}}{x}$与直线y=k2x交于A(-1,m)、B(n,-2)两点