题目内容
15.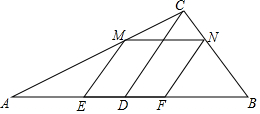 如图,已知Rt△ABC中,∠C=90°,D是中点,AE=EF=FB,EM∥DC∥FM.求证:四边形EFNM是菱形.
如图,已知Rt△ABC中,∠C=90°,D是中点,AE=EF=FB,EM∥DC∥FM.求证:四边形EFNM是菱形.
分析 根据直角三角形中线的性质得到CD=AD=BD,根据平行线分线段成比例的性质得到ME=NF=EF,再根据平行四边形的判定,菱形的判定即可求解.
解答 证明:∵Rt△ABC中,∠C=90°,D是中点,
∴CD=AD=BD,
∵AE=EF=FB,EM∥DC∥FM,
∴ME=NF=EF=$\frac{2}{3}$CD,
∵EM∥FM,
∴四边形EFNM是平行四边形,
∵ME=NF,
∴四边形EFNM是菱形.
点评 考查了菱形的判定,直角三角形中线的性质,平行线分线段成比例的性质,平行四边形的判定,关键是得到ME=NF=EF.

练习册系列答案
相关题目
17.下列四个几何体中,主视图与俯视图相同的是( )
| A. |  | B. |  | C. |  | D. |  |
5.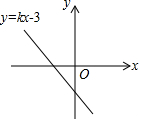 若函数y=kx-3的图象如图所示,则一元二次方程x2+x+k-1=0根的存在情况是( )
若函数y=kx-3的图象如图所示,则一元二次方程x2+x+k-1=0根的存在情况是( )
 若函数y=kx-3的图象如图所示,则一元二次方程x2+x+k-1=0根的存在情况是( )
若函数y=kx-3的图象如图所示,则一元二次方程x2+x+k-1=0根的存在情况是( )| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |

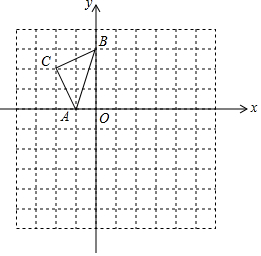 如图,在已知的平面直角坐标系中,△ABC的顶点都在正方形网格的格点上,若A,B两点的坐标分别是A(-1,0),B(0,3).
如图,在已知的平面直角坐标系中,△ABC的顶点都在正方形网格的格点上,若A,B两点的坐标分别是A(-1,0),B(0,3).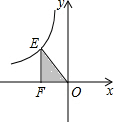 位于第二象限的点E在反比例函数y=$\frac{k}{x}$的图象上,点F在x轴的负半轴上,O是坐标原点,若FO⊥EF,△EOF的面积等于2,则k的值是( )
位于第二象限的点E在反比例函数y=$\frac{k}{x}$的图象上,点F在x轴的负半轴上,O是坐标原点,若FO⊥EF,△EOF的面积等于2,则k的值是( )