题目内容
9.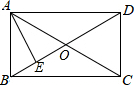 如图,矩形ABCD的对角线交于点O,∠AOB=36°,AE平分∠BAC交BD于点E,若AC=4,则AB的长度为( )
如图,矩形ABCD的对角线交于点O,∠AOB=36°,AE平分∠BAC交BD于点E,若AC=4,则AB的长度为( )| A. | $\sqrt{5}$-2 | B. | 5-$\sqrt{5}$ | C. | $\sqrt{5}$-1 | D. | 4-$\sqrt{5}$ |
分析 如图,设AB=x.首先证明AB=AE=OE=x,再证明△BAE∽△BOA,可得AB2=BE•BO,可得x2=2(2-x),求出x即可.
解答 解:如图,设AB=x.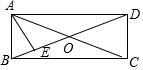
∵四边形ABCD是矩形,
∴OA=OB=OC=OD=2,
∵∠AOB=36°,AE平分∠BAO,
∴∠OAB=∠OBA=72°,∠BAE=∠EAO=36°,
∴∠ABE=∠AEB=72°,
∴AB=AE=OE=x,
∴∠BAE=∠BOA,
∵∠ABE=∠ABO,
∴△BAE∽△BOA,
∴AB2=BE•BO,
∴x2=2(2-x),
∴x2+2x-4=0,
∴x=-1+$\sqrt{5}$或-1-$\sqrt{5}$(舍弃),
∴AB=$\sqrt{5}$-1,
故选C.
点评 本题考查矩形的性质.相似三角形的判定和性质、一元二次方程等知识,解题的关键是正确寻找相似三角形解决问题,学会构建方程解决问题,属于中考常考题型.

练习册系列答案
相关题目
19.若长方形的长为2a+1,宽为3a2-2a+1,则这个长方形的面积是( )
| A. | 6a3+2a2+1 | B. | 6a3-a2+1 | C. | 6a3+1 | D. | 6a3-1 |
18.下列命题的逆命题是真命题的是( )
| A. | 对顶角相等 | B. | 全等三角形的面积相等 | ||
| C. | 两直线平行,内错角相等 | D. | 等边三角形是等腰三角形 |
19.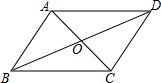 如图,?ABCD的对角线相交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线的和是( )
如图,?ABCD的对角线相交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线的和是( )
 如图,?ABCD的对角线相交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线的和是( )
如图,?ABCD的对角线相交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线的和是( )| A. | 18 | B. | 28 | C. | 36 | D. | 46 |
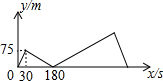 A、B两地相距1500米,甲从A地出发慢速跑向B地,30秒后乙从A地出发快速跑向B地,乙到B地后原地休息,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示.
A、B两地相距1500米,甲从A地出发慢速跑向B地,30秒后乙从A地出发快速跑向B地,乙到B地后原地休息,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示.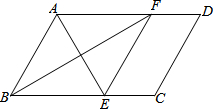 如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.
如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F. 已知,在平面直角坐标系中,正方形A1B1C1A2与正方形A2B2C2A3是以原点O为位似中心的位似图形,且相似比为$\frac{1}{2}$,点A1,A2,A3在x轴上,延长A3C2交射线OB1于点B3,以A3B3为边长作正方形A3B3C3A4;延长A4C3交射线OB1于点B4,以A4B4为边长作正方形A4B4C4A5…,若OA1=2,则正方形AnBnCnAn+1的面积为( )
已知,在平面直角坐标系中,正方形A1B1C1A2与正方形A2B2C2A3是以原点O为位似中心的位似图形,且相似比为$\frac{1}{2}$,点A1,A2,A3在x轴上,延长A3C2交射线OB1于点B3,以A3B3为边长作正方形A3B3C3A4;延长A4C3交射线OB1于点B4,以A4B4为边长作正方形A4B4C4A5…,若OA1=2,则正方形AnBnCnAn+1的面积为( )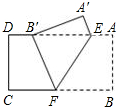 如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处,若AE=3,AB=4,∠EFB=60°,则四边形A′B′FE的周长是=17.
如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处,若AE=3,AB=4,∠EFB=60°,则四边形A′B′FE的周长是=17.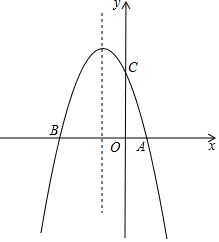 如图,抛物线y=-x2+bx+c与x轴交于A(1,0),B(-3,0)
如图,抛物线y=-x2+bx+c与x轴交于A(1,0),B(-3,0)