题目内容
16．在△ABC中，∠A=36°，∠B=2∠C，试判断△ABC的形状．分析 首先根据三角形的内角和定理，求出∠B、∠C的度数和是多少；然后根据∠B=2∠C，用∠B、∠C的度数和除以3，求出∠C的度数，进而求出∠B的度数，判断出△ABC的形状即可．
解答 解：∵∠A=36°，
∴∠B+∠C=180°-36°=144°，
又∵∠B=2∠C，
∴∠C=144°÷（1+2）=144°÷3=48°，
∴∠B=2∠C=2×48°=96°，
∵∠B=96°＞90°，
∴△ABC是钝角三角形．
点评 （1）此题主要考查了三角形的内角和定理，要熟练掌握，解答此题的关键是要明确：三角形的内角和是180°．
（2）此题还考查了三角形的分类，要熟练掌握，解答此题的关键是分别求出∠B、∠C的度数各是多少．
练习册系列答案
相关题目
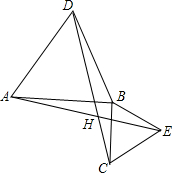如果两个等边三角形△ABD和△BCE，连接AE与CD，证明：
如图，Rt△ABC中，∠ACB=90°，∠CAB=20°，∠ACB的平分线与外角∠ABD的平分线交于点E，连接AE，则∠AEB的度数为45°．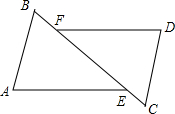
如图，如果BF=CE，需要补充一个条件，就能使△ABE≌△DCF．小明给出了下面四个答案：①AE=DF；②AE∥DF；③AB∥DC；④∠A=∠D，其中正确的是（ ）