题目内容
3．
抛物线y=-x2+bx+c的部分图象如图所示，对称轴是直线x=-1，与x轴交于点（1，0），若y＜0，则x的取值范围是（ ）| A． | x＞0 | B． | x＞1 | C． | x＜-3或x＞1 | D． | D-3＜x＜1 |
分析 根据二次函数的对称性求出抛物线与x轴的另一交点坐标，然后写出x轴下方部分的x的取值范围即可．
解答 解：设抛物线与x轴的另一交点坐标为（x，0），
则$\frac{x+1}{2}$=-1，
解得x=-3，
∴另一交点坐标为（-3，0），
∴y＜0时，x的取值范围是x＜-3或x＞1．
故选C．
点评 本题考查了二次函数与不等式，主要利用了二次函数的对称性，此类题目利用数形结合的思想求解更加简便．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
13．
如图，无法保证△ADE与△ABC相似的条件是（ ）
如图，无法保证△ADE与△ABC相似的条件是（ ）| A． | ∠1=∠C | B． | ∠A=∠C | C． | ∠2=∠B | D． | $\frac{AD}{AC}=\frac{AE}{AB}$ |
如图，在△ABC中，∠BAC=90°，AB=AC，∠ABD=∠BAD=15°，求证：AC=DC．
18．在Rt△ABC中，∠C=90°，tanA=$\sqrt{2}$，则sinB=（ ）
| A． | $\frac{\sqrt{3}}{3}$ | B． | $\frac{\sqrt{6}}{3}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\sqrt{3}$ |
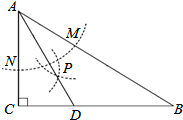如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于$\frac{1}{2}$MN的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D，则下列说法中正确的个数是（ ）
12．已知等式ax=ay，下列变形不正确的是（ ）
| A． | x=y | B． | ax+1=ay+1 | C． | 2ax=2ay | D． | 3-ax=3-ay |
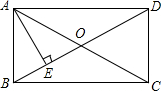如图，在矩形ABCD中，AE⊥BD于E，AC与BD相交于O点，DE=3BE．