Question

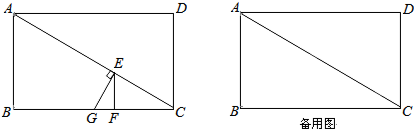
4．已知：如图，矩形ABCD，AB=4，∠ACB=30°．点E从点C出发，沿折线CA-AD以每秒一个单位长度的速度运动，过点E作EF∥CD交BC于点F，同时过点E作EG⊥AC交直线BC于点G，设运动的时间为t，△EFG与△ABC重叠部分的面积为S，当点E运动到点D时停止运动．
（1）当点B与点G重合时，求此时t的值；
（2）直接写出S与t之间的函数关系式和相应的自变量取值范围；
（3）当t=4时，将△EFG绕点E顺时针旋转一个角度α（0°≤α≤90°），∠GEF的两边分别交矩形的边于点M，点N．当△MEN为等腰三角形时，求此时△MEN的面积．

Answer 1

分析 （1）当点B与点G第一次重合时，当点B与点G第二次重合时，两种情况结合图形特征求解；
（2）分$0≤t＜6，6≤t＜8，8≤t＜8+\frac{4\sqrt{3}}{3}，8+\frac{4\sqrt{3}}{3}≤t≤8+4\sqrt{3}$，根据相似三角形的性质和三角形的面积公式求解即可；
（3）t=4时，此时点E在AC的中点，当△MEN为等腰三角形时，共有以下三种情况，0≤α＜30°；30°≤α＜60°；60≤α≤90°．

解答 解：（1）当点B与点G第一次重合时，如图1，
∵AB=4，∠ACB=30°，
∴BC=$4\sqrt{3}$，
∴CE=$2\sqrt{3}×\sqrt{3}=6$；
∴t=6，
当点B与点G第二次重合时，如图2：
∵AD∥BC，
∴∠DAC=∠ACB=30°，
∵AB=4，
∴AC=2AB=8，
∵BE⊥AC，
∴∠ABE=30°，
∴tan30°=$\frac{AE}{AB}$，
∴AE=$\frac{4}{3}\sqrt{3}$，
∴点E走过的路程为8+$\frac{4}{3}\sqrt{3}$，
∴t=8+$\frac{4}{3}\sqrt{3}$；

（2）当0≤t＜6时，如图3，
此时，△EFG与△ABC重叠部分为△EFG，
∵CE=t，∠ACB=30°，
∴EF=$\frac{1}{2}$t，
∵∠GEF=∠ACB=30°，
∴tan30°=$\frac{GF}{EF}$，
∴GF=$\frac{\sqrt{3}}{6}$t，
∴S=$\frac{1}{2}$EF•GF=$\frac{\sqrt{3}}{24}$t²，
当6≤t＜8时，设GE与AB交于点H，如图4，
此时，△EFG与△ABC重叠部分为梯形HBFE，
∵CE=t，
∴CF=$\frac{1}{2}$$\sqrt{3}$t，
∴BF=BC-CF=4$\sqrt{3}$-$\frac{\sqrt{3}}{2}$t，
∴BG=GF-BF=$\frac{4\sqrt{3}}{6}$t-4$\sqrt{3}$，
∵∠GHB═∠GEF=∠ACB=30°，
∴HB=$\sqrt{3}$BG=2t-12，
∴S=$\frac{1}{2}$EF•GF-$\frac{1}{2}$BG•HB=-$\frac{5\sqrt{3}}{8}$t²+8$\sqrt{3}$t-24$\sqrt{3}$，
当8≤t＜8+$\frac{4}{3}\sqrt{3}$时，设GE与AB交于点H，如图5，
此时，△EFG与△ABC重叠部分为梯形HBFE，
∵AB=EF=4，
∴GF=$\frac{EF}{\sqrt{3}}$=$\frac{4}{3}\sqrt{3}$，
∵BF=AE，
∴BF=t-8，
∴BG=GF-BF=8+$\frac{4}{3}\sqrt{3}$-t，
∴S=$\frac{1}{2}$GF•EF-$\frac{1}{2}$BG•HB=-$\frac{13\sqrt{3}}{24}$t²+（$\frac{26\sqrt{3}}{3}$+4）t-32-$\frac{104\sqrt{3}}{3}$，
当8+$\frac{4\sqrt{3}}{3}$≤t≤8+4$\sqrt{3}$时，
设EG与AC交于点H，EF与AC交于点I，如图6
此时，△EFG与△ABC重叠部分为四边形HGFI，
∵AE=t-8，∠DAC=∠ACB=30°，
∴EI=$\frac{AE}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$（t-8），
∵∠HEI=30°，
∴HI=$\frac{1}{2}$EI=$\frac{\sqrt{3}}{6}$（t-8），
EH=$\sqrt{3}$HI=$\frac{1}{2}$（t-8），
∴S=$\frac{1}{2}$EF•GF-$\frac{1}{2}$EH•HI=-$\frac{\sqrt{3}}{24}$t²+$\frac{2\sqrt{3}}{3}$t；

（3）t=4时，此时点E在AC的中点处，即CE=4，
当0≤α＜30°时，如图7，
此时，∠EMN=∠MEN=30°时，△MEN为等腰三角形，
此时点M与B重合，
∴EF=$\frac{1}{2}$CE=2，
∵∠EMN=∠ENM=30°，
∴∠ENF=30°，
∴EN=$\frac{EF}{cos30°}$=$\frac{4\sqrt{3}}{3}$，
∴MN=EN=$\frac{4\sqrt{3}}{3}$，
∴△MNE的面积为$\frac{1}{2}$MN•EF=$\frac{4\sqrt{3}}{3}$，
当30°≤α＜60°时，
过点M作MK⊥AC于点K，
过点E作EI⊥AB于点I，
过点N作NP⊥ME于点P，
若ME=NE时，如图8，
易求得：EI=2$\sqrt{3}$，AI=2，AE=4，EF=2，
∵∠MNE=30°，
∴∠MEI=90°-∠MNE-∠NEF=60°-∠NEF，
∵∠AEI=30°，
∴∠KME=90°-∠AEI-∠MEI=∠NEF
在△MEK与△ENF中，
$\left\{\begin{array}{l}{∠MKE=∠EFN}\\{∠KME=∠NEF}\\{ME=NE}\end{array}\right.$，
∴△MEK≌△ENF（AAS），
∴MK=EF=2，
∵$\frac{1}{2}$AM•EI=$\frac{1}{2}$AE•MK，
∴AM=$\frac{4}{3}$$\sqrt{3}$，
∴MI=AM-AI=$\frac{4\sqrt{3}-6}{3}$，
由勾股定理可求得：ME²=（2$\sqrt{3}$）²+（$\frac{4\sqrt{3}-6}{3}$）²=$\frac{64-16\sqrt{3}}{3}$，
∵∠MEN=30°，
∴NP=$\frac{1}{2}$NE=$\frac{1}{2}ME$，
∴△MEN的面积为$\frac{1}{2}$ME•NP=$\frac{1}{4}$ME²=$\frac{16-4\sqrt{3}}{3}$；
若MN=NE时，如图9，
同理可得：∠KME=∠NEF，
∴△MEK∽△ENF，
∵∠MEN=30°，
∴NP=$\frac{1}{2}$NE，
∴PE=$\frac{\sqrt{3}}{2}$NE，
∵MN=NE，NP⊥ME
∴ME=2PE=$\sqrt{3}$NE，
∴$\frac{ME}{NE}=\frac{MK}{EF}$，
∴$\sqrt{3}$=$\frac{MK}{2}$，
∴MK=2$\sqrt{3}$，
∵$\frac{1}{2}$AM•EI=$\frac{1}{2}$AE•MK，
∴AM=4，
此时M与B重合，此情况舍去；
当60≤α≤90°时，如图10
此时只能ME=NE，
∵EI⊥AB，
∴∠NEI=$\frac{1}{2}$∠MEN=15°，
∴tan15°=$\frac{NI}{EI}$，
∴NI=EI•tan15°=4$\sqrt{3}$-6，
∴MN=2NI=8$\sqrt{3}$-12，
∴△MNE的面积为$\frac{1}{2}$MN•EI=24-12$\sqrt{3}$
综上所述，当△MEN为等腰三角形时，此时△MEN的面积为$\frac{4\sqrt{3}}{3}$或$\frac{16-4\sqrt{3}}{3}$或24-12$\sqrt{3}$．

点评 本题考查四边形的综合题，涉及矩形的性质，直角三角形的性质，全等三角形的判定与性质，相似三角形的判定与性质，等腰三角形的性质，分类讨论的思想，综合程度较高，需要学生灵活运用所学知识进行解答．