题目内容
9. 如图,在平面直角坐标系中,已知点A(0,3$\sqrt{3}$),B(3,0),点C在线段AB上,且点C的横坐标为1.若点P为y轴上的一个动点,则PC+PB的最小值是( )
如图,在平面直角坐标系中,已知点A(0,3$\sqrt{3}$),B(3,0),点C在线段AB上,且点C的横坐标为1.若点P为y轴上的一个动点,则PC+PB的最小值是( )| A. | 2$\sqrt{7}$ | B. | 4 | C. | 3$\sqrt{7}$ | D. | 1+2$\sqrt{7}$ |
分析 求出B点关于y轴的对称点B′,连接B′C,交y轴于点P,则P即为所求点,利用两点间的距离公式即可求解.
解答  解:设C的纵坐标为y,
解:设C的纵坐标为y,
∵点A(0,3$\sqrt{3}$),B(3,0),点C在线段AB上,且点C的横坐标为1,
∴$\frac{3\sqrt{3}-y}{3\sqrt{3}}$=$\frac{1}{3}$,
∴y=2$\sqrt{3}$,
∴C(1,2$\sqrt{3}$),
如图所示:作点B关于y轴的对称点B′(-3,0),连接B′C,交y轴于点P,则P即为所求点,即当三点在一条直线上时有最小值,
即PC+PB=B′C=$\sqrt{(-3-1)^{2}+(0-2\sqrt{3})^{2}}$=2$\sqrt{7}$.
故选A.
点评 本题题考查的是最短线路问题及两点间的距离公式,解答此题的关键是熟知两点之间线段最短的知识.

练习册系列答案
相关题目
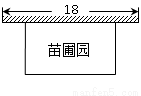
 ,求
,求 的值。(先化简再求值)
的值。(先化简再求值) 是一个完全平方式,则a的值为( )
是一个完全平方式,则a的值为( )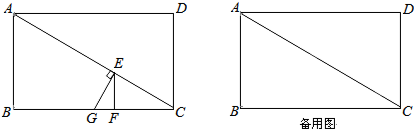
 气象台测得台风中心在A城正西方向600KM的B处,以每小时200KM的速度向北偏东60度BF方向移动,距离台风中心500KM的范围内是受台风影响的区域.
气象台测得台风中心在A城正西方向600KM的B处,以每小时200KM的速度向北偏东60度BF方向移动,距离台风中心500KM的范围内是受台风影响的区域.