题目内容
8．下列各数中，为不等式组$\left\{\begin{array}{l}{x-4＜0}\\{2x-3＞0}\end{array}\right.$的解的是（ ）| A． | -1 | B． | 2 | C． | 0 | D． | 4 |
分析 首先计算出两个不等式的解集，再根据大小小大中间找确定不等式组的解集．
解答 解：$\left\{\begin{array}{l}{x-4＜0①}\\{2x-3＞0②}\end{array}\right.$，
由①得：x＜4，
由②得：x＞$\frac{3}{2}$，
不等式组的解集为：$\frac{3}{2}$＜x＜4，
故选：B．
点评 此题主要考查了一元一次不等式组的解法以及不等式组的解，关键是掌握解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．
练习册系列答案
相关题目
19．已知$\frac{1}{x}$-$\frac{1}{y}$=3，则分式$\frac{2x+3xy-2y}{x-2xy-y}$的值为（ ）
| A． | $\frac{3}{5}$ | B． | -3 | C． | 9 | D． | -$\frac{9}{5}$ |
20．下列比较大小正确的是（ ）
| A． | $\root{3}{6}$＜1 | B． | $\root{3}{-8}$=$\root{3}{8}$ | C． | $\sqrt{15}$＞4 | D． | $\sqrt{3}$-2＞-$\frac{\sqrt{3}}{2}$ |
17．
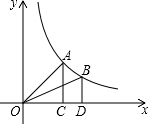如图，过反比例函数y=$\frac{1}{x}$（x＞0）的图象上任意两点A、B分别作x轴的垂线，垂足分别为C、D，连接OA、OB，设△AOC和△BOD的面积分别是S1、S2，比较它们的大小，可得（ ）
如图，过反比例函数y=$\frac{1}{x}$（x＞0）的图象上任意两点A、B分别作x轴的垂线，垂足分别为C、D，连接OA、OB，设△AOC和△BOD的面积分别是S1、S2，比较它们的大小，可得（ ）| A． | S1＞S2 | B． | S1=S2 | ||
| C． | S1＞S2 | D． | 大小关系不能确定 |
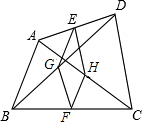如图，在四边形ABCD中，AB=DC，E、F分别是AD、BC的中点，G、H分别是对角线BD、AC的中点．