题目内容
17．
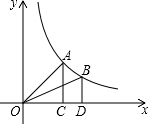如图，过反比例函数y=$\frac{1}{x}$（x＞0）的图象上任意两点A、B分别作x轴的垂线，垂足分别为C、D，连接OA、OB，设△AOC和△BOD的面积分别是S1、S2，比较它们的大小，可得（ ）| A． | S1＞S2 | B． | S1=S2 | ||
| C． | S1＞S2 | D． | 大小关系不能确定 |
分析 根据反比例函数的几何意义，直接求出S1、S2的值即可进行比较．
解答 解：由于A、B均在反比例函数y=$\frac{1}{x}$的图象上，
且AC⊥x轴，BD⊥x轴，
则S1=$\frac{1}{2}$；
S2=$\frac{1}{2}$．
故S1=S2．
故选：B．
点评 此题考查了反比例函数k的几何意义，找到相关三角形，求出k的一半即为三角形的面积．
练习册系列答案
阳光课堂同步练习系列答案
相关题目
5．2sin60°的值等于（ ）
| A． | $\sqrt{3}$ | B． | 2 | C． | 1 | D． | $\sqrt{2}$ |