题目内容
20. 如图,已知AD是△ABC的中线,AB=6,AC=4,△ACD的面积为6,那么△ABC的面积为12,△ABD与△ACD的周长之差是2,BC边的长可以为5(写出一个即可)
如图,已知AD是△ABC的中线,AB=6,AC=4,△ACD的面积为6,那么△ABC的面积为12,△ABD与△ACD的周长之差是2,BC边的长可以为5(写出一个即可)
分析 根据△ABC的面积=2△ACD的面积,根据三角形的中线的定义可得BD=CD,然后求出△ABD与△ACD的周长之差=AB-AC,根据三角形的三边关系即可得到结论.
解答 解:∵AD是△ABC的中线,
∴△ABC的面积=2△ACD的面积=12,
∵AD为中线,
∴BD=CD,
∴△ABD与△ACD的周长之差=(AB+AD+BD)-(AC+AD+CD)=AB-AC,
∵AB=6,AC=4,
∴△ABD与△ACD的周长之差=6-4=2;
∵6-4<BC<6+4,
∴BC边的长可以为5.
故答案为:12,2,5.
点评 本题考查了三角形的面积,三角形的角平分线、中线和高,熟记概念并求出两个三角形的周长的差等于两边的差是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.-|-$\frac{3}{5}$|的负倒数是( )
| A. | $-\frac{5}{3}$ | B. | $\frac{5}{3}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
8.关于x的一元二次方程(a+1)x2-4x+1=0有两个不相等的实数根,则a的取值范围是( )
| A. | a>3 | B. | a<3且a≠-1 | C. | a<3 | D. | a≥3且a≠-1 |

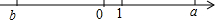 数轴上有b,0,1,a的四个数,如图所示,已知|a|=|b|,化简:|b+1|+|$\frac{a}{b}$|-|a+b|.
数轴上有b,0,1,a的四个数,如图所示,已知|a|=|b|,化简:|b+1|+|$\frac{a}{b}$|-|a+b|.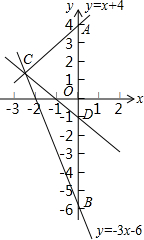 如图所示,设函数y=x+4的图象与y轴交于点A,函数y=-3x-6的图象与y轴交于点B,两个函数的图象交于点C,求通过线段AB的中点D及点C的一次函数表达式.
如图所示,设函数y=x+4的图象与y轴交于点A,函数y=-3x-6的图象与y轴交于点B,两个函数的图象交于点C,求通过线段AB的中点D及点C的一次函数表达式.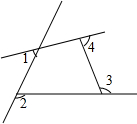 如图,∠2+∠3+∠4=318°,则∠1=42°.
如图,∠2+∠3+∠4=318°,则∠1=42°.