题目内容
5.若∠A为锐角,化简$\sqrt{si{n}^{2}A-2sinA+1}$=1-sinA.分析 先利用完全平方公式得到原式=$\sqrt{(sinA-1)^{2}}$,再利用二次根式的性质化简得原式=|sinA-1|,然后利用锐角三角函数的定义得到0<sinA<1,于是根据绝对值的意义去绝对值即可.
解答 解:原式=$\sqrt{(sinA-1)^{2}}$
=|sinA-1|,
∵∠A为锐角,
∴0<sinA<1,
∴原式=1-sinA.
故答案为1-sinA.
点评 本题考查了二次根式的性质与化简:会应用$\sqrt{{a}^{2}}$=|a|进行二次根式的化简.也考查了锐角三角函数的定义.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 a、b、c在数轴上的位置如图所示,则:
a、b、c在数轴上的位置如图所示,则: 如图所示,已知AC=DE,AF=DB,∠A=∠D,△ABC和△DFE全等吗?并说明理由.
如图所示,已知AC=DE,AF=DB,∠A=∠D,△ABC和△DFE全等吗?并说明理由.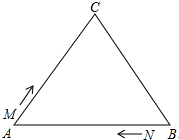 如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.
如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动. △ABC中,D在BC上,且AB=AC=BD,∠1=30°,求∠2的度数.
△ABC中,D在BC上,且AB=AC=BD,∠1=30°,求∠2的度数.