题目内容
13.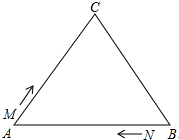 如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.
如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.(1)点M、N运动多少秒后,△AMN为等腰三角形?
(2)点M、N运动多少秒后,△AMN为直角三角形?
分析 (1)根据题意设点M、N运动t秒后,可得到等边三角形△AMN,然后表示出AM,AN的长,由于∠A等于60°,所以只要AM=AN三角形ANM就是等边三角形;
(2)根据题意设点M、N运动t秒后,可得到直角三角形△AMN,然后表示出AM,AN的长,由于∠A等于60°,所以只要AM=2AN或2AM=AN三角形ANM就是直角三角形.
解答 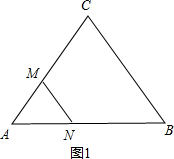 解:(1)∵AB=BC=AC,
解:(1)∵AB=BC=AC,
∴△ABC是等边三角形,
∴∠A=60°,
∵△AMN为等腰三角形,
∴△AMN是等边三角形,
设点M、N运动t秒后,可得到等边三角形△AMN,如图1,
AM=t×1=t,AN=AB-BN=12-2t,
∵三角形△AMN是等边三角形,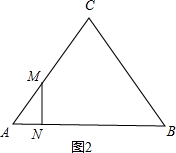
∴t=12-2t,
解得t=4,
∴点M、N运动4秒后,可得到等腰三角形△AMN.
(2)①当∠ANM=90°时,
∵∠A=60°,
∴∠AMN=30°,如图2,
∴AM=2AN,
设点M、N运动t秒后,可得到直角三角形△AMN,如图2,
AM=t×1=t,AN=AB-BN=12-2t,
∴t=2(12-2t),
∴t=$\frac{24}{5}$;
②当∠AMN=90°时,
∵∠A=60°,
∴∠ANM=30°,
∴2AM=AN,
∴2t=12-2t,
∴t=3,
∴点M、N运动$\frac{24}{5}$或3秒后,△AMN为直角三角形.
点评 此题主要考查了等边三角形的性质及判定,关键是根据题意设出未知数,理清线段之间的数量关系.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
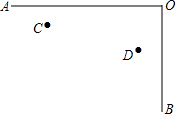 城北中学八(2)班举行文艺晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子,OB桌面上摆满了糖果,站在C处的学生小明先到AO桌面上拿桔子,再到OB桌面上拿糖果,然后回到D处座位上,请你帮助他设计一条行走路线,使其所走的总路程最短.
城北中学八(2)班举行文艺晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子,OB桌面上摆满了糖果,站在C处的学生小明先到AO桌面上拿桔子,再到OB桌面上拿糖果,然后回到D处座位上,请你帮助他设计一条行走路线,使其所走的总路程最短.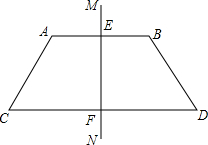 如图,MN垂直平分线段AB,CD,垂足分别为E,F,求证:AC=BD,∠C=∠D.
如图,MN垂直平分线段AB,CD,垂足分别为E,F,求证:AC=BD,∠C=∠D. 如图,△ABC是一个等腰三角形钢架,现要在横梁BC上确定一点D,使△ABD≌△ACD,点D的位置应当选在何处?为什么?
如图,△ABC是一个等腰三角形钢架,现要在横梁BC上确定一点D,使△ABD≌△ACD,点D的位置应当选在何处?为什么?