题目内容
8.已知△ABC的两条角平分线BD,CE交于点O,OD=OE,∠ABC=70°,则∠A=60°.分析 根据三角形的内角和等于180°求出∠ABC+∠ACB=180°-∠A,再根据角平分线的性质求出∠OBC+∠OCB$\frac{1}{2}$(∠ABC+∠ACB),然后利用三角形的内角和等于180°列式计算即可求出∠BOC=∠EOD=90°+$\frac{1}{2}∠$A;连接OA,作OF⊥AB于点F,OG⊥AC于点G,OH⊥BC于点H,根据角平分线上的点到角的两边的距离相等可得OF=OG=OH,利用“HL”证明△EOF和△DOG全等,得出∠EOF=∠DOG,即可证得∠FOG=∠EOD,由∠A+∠FOG=180°,得出∠A+∠EOD=180°,从而得出∠A+90°+$\frac{1}{2}∠$A=180°,解得∠A=60°.
解答  解:∴∠ABC+∠ACB=180°-∠A,
解:∴∠ABC+∠ACB=180°-∠A,
∵△ABC的两条角平分线BD、CE交于O,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-$\frac{1}{2}$(∠ABC+∠ACB)=180°-$\frac{1}{2}$(180°-∠A)=90°+$\frac{1}{2}∠$A,
∴∠EOD=90°+$\frac{1}{2}∠$A,
连接OA,作OF⊥AB于点F,OG⊥AC于点G,OH⊥BC于点H,
∵△ABC的两条角平分线BD、CE交于O,
∴OF=OG=OH,
在RT△EOF和RT△DOG中,
$\left\{\begin{array}{l}{OF=OG}\\{OE=OD}\end{array}\right.$
∴△EOF≌△DOG(HL),
∴∠EOF=∠DOG,
∴∠FOG=∠EOD,
∵OF⊥AB,OG⊥AC,
∴∠A+∠FOG=180°,
∴∠A+∠EOD=180°,
∴∠A+90°+$\frac{1}{2}∠$A=180°,
∴∠A=60°.
故答案为60°.
点评 本题考查了角平分线的性质,全等三角形的判定与性质,作出辅助线,推出∠A+∠EOD=180°,从而得到∠A+90°+$\frac{1}{2}∠$A=180°是关键,也是解决本题的难点.

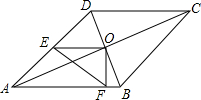 如图,在?ABCD中,对角线AC、BD相交于点O,点E、F分别是边AD、AB上的点,连结OE、OF、EF.若AB=7,BC=5$\sqrt{2}$,∠DAB=45°,则△OEF周长的最小值是$\frac{13\sqrt{2}}{2}$.
如图,在?ABCD中,对角线AC、BD相交于点O,点E、F分别是边AD、AB上的点,连结OE、OF、EF.若AB=7,BC=5$\sqrt{2}$,∠DAB=45°,则△OEF周长的最小值是$\frac{13\sqrt{2}}{2}$.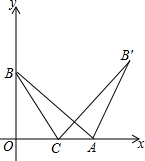 如图,在平面直角坐标系xOy中,点A、B分别在x轴,y轴的正半轴上,且OA=OB,将线段AB绕点A顺时针旋转60°得到AB′,C是x轴上一点,BC+B′C的值最小是B′D,∠OCB=60°.
如图,在平面直角坐标系xOy中,点A、B分别在x轴,y轴的正半轴上,且OA=OB,将线段AB绕点A顺时针旋转60°得到AB′,C是x轴上一点,BC+B′C的值最小是B′D,∠OCB=60°.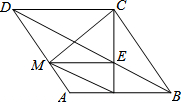 己知:如图,在菱形ABCD中,点M、N分别在边AD、AB,∠DCM=∠BCN,CN与BD交于点E.
己知:如图,在菱形ABCD中,点M、N分别在边AD、AB,∠DCM=∠BCN,CN与BD交于点E.